
科目:初中数学 来源:江苏省南通市海安县八校联考2012届九年级10月阶段测试数学试题 题型:013
在 中,无理数的个数为
中,无理数的个数为
A.44个
B.1966个
C.1967个
D.1968个
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
| A、调查的方式是普查 | B、本地区约有15%的成年人吸烟 | C、样本是150个吸烟的成年人 | D、本地区只有850个成年人不吸烟 |
科目:初中数学 来源: 题型:
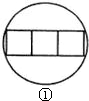
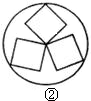
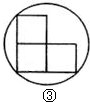
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
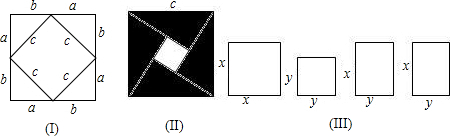
科目:初中数学 来源: 题型:
| 1 | 2 |
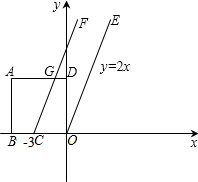 运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S.
运动时间为t秒,正方形被夹在直线OE与CF间的部分的面积为S.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com