练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知△ABC中，∠ACB=90。，以△ABC的各边为边在△ABC外作三个正方形，S1，S2，S3分别表示这三个正方形的面积，S1=81，S2=225，则S3=（     ）


    A.300
    B.306
    C.144
    D.114
    C
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：江苏期中题 题型：单选题

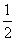    如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：
    ①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S四边形CDFE=S△ABC。
    上述结论中始终正确的有

    [     ]

    A.①②③
    B.②③④
    C.①③④
    D.①②④

    查看答案和解析>>

    科目：初中数学 来源：浙江省中考真题 题型：填空题

    如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC、BC为直径作半圆，面积分别为S1、S2，则S+S2的值等于（    ）。

    查看答案和解析>>

    科目：初中数学 来源：2013年江苏省东台市实验中学中考数学模拟试卷（带解析） 题型：解答题

    已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点，点P、Q分别从点A、C出发，沿AC、CB以每秒1个单位的速度运动，到达点C、B后停止。连结PQ、点D是PQ中点，连结CD并延长交AB于点E.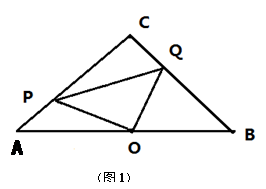

    （1）试说明：△POQ是等腰直角三角形；
    （2）设点P、Q运动的时间为t秒，试用含t的代数式来表示△CPQ的面积S，并求出
    S的最大值；
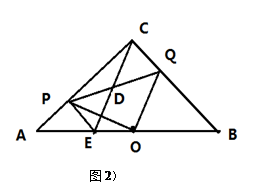
    （3）如图2，点P在运动过程中，连结EP、EQ，问四边形PEQC是什么四边形，并说明理由；
    （4）求点D运动的路径长（直接写出结果）.

    查看答案和解析>>

    科目：初中数学 来源：2013年江苏省东台市中考数学模拟试卷（解析版） 题型：解答题

    已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点，点P、Q分别从点A、C出发，沿AC、CB以每秒1个单位的速度运动，到达点C、B后停止。连结PQ、点D是PQ中点，连结CD并延长交AB于点E.

    （1）试说明：△POQ是等腰直角三角形；

    （2）设点P、Q运动的时间为t秒，试用含t的代数式来表示△CPQ的面积S，并求出

    S的最大值；

    （3）如图2，点P在运动过程中，连结EP、EQ，问四边形PEQC是什么四边形，并说明理由；

    （4）求点D运动的路径长（直接写出结果）.

     

    查看答案和解析>>

    科目：初中数学 来源：北京期末题 题型：解答题

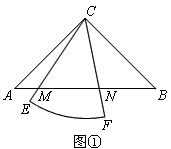
    已知：如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=4，以AC为直径的交AB于点D，点E是BC的中点，OB，DE相交于点F。
    （1）求证：是⊙O的切线；
    （2）求EF：FD的值。

    查看答案和解析>>

    科目：初中数学 来源：北京模拟题 题型：证明题

    已知：如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O交AB于点D，过点D作⊙O的切线DE交BC于点E。
    求证：BE=CE。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点，点P、Q分别从点A、C出发，沿AC、CB以每秒1个单位的速度运动，到达点C、B后停止。连结PQ、点D是PQ中点，连结CD并延长交AB于点E.

    （1）       试说明：△POQ是等腰直角三角形；

    （2）       设点P、Q运动的时间为t秒，试用含t的代数式来表示△CPQ的面积S，并求出

    S的最大值；

    （3）       如图2，点P在运动过程中，连结EP、EQ，问四边形PEQC是什么四边形，并说明理由；

    （4）       求点D运动的路径长（直接写出结果）.

     


                   

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点，点P、Q分别从点A、C出发，沿AC、CB以每秒1个单位的速度运动，到达点C、B后停止。连结PQ、点D是PQ中点，连结CD并延长交AB于点E.

    （1）试说明：△POQ是等腰直角三角形；
    （2）设点P、Q运动的时间为t秒，试用含t的代数式来表示△CPQ的面积S，并求出
    S的最大值；
    （3）如图2，点P在运动过程中，连结EP、EQ，问四边形PEQC是什么四边形，并说明理由；
    （4）求点D运动的路径长（直接写出结果）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点，点P、Q分别从点A、C出发，沿AC、CB以每秒1个单位的速度运动，到达点C、B后停止。连结PQ、点D是PQ中点，连结CD并延长交AB于点E.

    （1）       试说明：△POQ是等腰直角三角形；

    （2）       设点P、Q运动的时间为t秒，试用含t的代数式来表示△CPQ的面积S，并求出S的最大值；

    （3）       如图2，点P在运动过程中，连结EP、EQ，问四边形PEQC是什么四边形，并说明理由；

    （4）       求点D运动的路径长（直接写出结果）.

    查看答案和解析>>

    科目：初中数学 来源：天津中考真题 题型：解答题

    已知Rt△ABC中，∠ACB=90°，CA=CB，有一个圆心角为45°，半径的长等于CA的扇形CEF绕点C旋转，且直线CE，CF分别与直线AB交于点M，N。
     
    （1）当扇形CEF绕点C在∠ACB的内部旋转时，如图1，求证：MN2=AM2+BN2；（思路点拨：考虑MN2=AM2+BN2符合勾股定理的形式，需转化为在直角三角形中解决，可将△ACM沿直线CE对折，得△DCM，连DN，只需证DN=BN，∠MDN=90°就可以了，请你完成证明过程。）
    （2）当扇形CEF绕点C旋转至图2的位置时，关系式MN2=AM2+BN2是否仍然成立？若成立，请证明；若不成立，请说明理由。

    查看答案和解析>>


    同步练习册答案