
| 矩形的周长为50,设它的长为x,宽为y,则y与x的函数关系为 |
A.y=-x +25 B.y=x+ 25 C.y=-x +50 D.y=x+50 |
科目:初中数学 来源:期末题 题型:单选题
科目:初中数学 来源:山东省期末题 题型:单选题
科目:初中数学 来源:期末题 题型:单选题
科目:初中数学 来源:云南省期末题 题型:单选题
科目:初中数学 来源:三点一测丛书九年级数学上 题型:044
实践与探索课上,老师布置了这样一道题:
有100米长的篱笆材料,想围成一矩形露天仓库,要求面积不小于600平方米,在场地的北面有一堵长50米的旧墙.有人用这个篱笆围一个长40米,宽10米的矩形仓库,但面积只有400平方米,不合要求.现在请你设计矩形仓库的长和宽,使它符合要求.
经过同学们一天的实践与思考,老师收到了如下几种设计方案:
(1)如果设矩形的宽为x米,则用于长的篱笆为![]() =(50-x)米,这时面积S=x(50-x)
=(50-x)米,这时面积S=x(50-x)
当S=600时,由x(50-x)=600,得x2-50x+600=0,解得x1=20,x2=30.
检验后知x=20符合要求.
(2)根据在周长相等的条件下,正方形面积大于矩形面积,所以设计成正方形仓库,它的边长为x米,则4x=100,x=25.这时面积达到625米,当然符合要求.
(3)如果利用场地北面的那堵旧墙,取矩形的长与旧墙平行,设与墙垂直的矩形一边长为x米,则另一边为100-2x,如图.
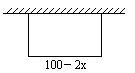
因为旧墙长50米,所以100-2x≤50.即x≥25米.若S=600平方米,则由x(100-2x)=600,即x2-50x+300=0,解得x1=25+5![]() ,x2=25-5
,x2=25-5![]() .根据x≥25,舍去x2=25-5
.根据x≥25,舍去x2=25-5![]() .
.
所以,利用旧墙,取矩形垂直于旧墙一边长为25+5![]() 米(约43米),另一边长约14米,符合要求.
米(约43米),另一边长约14米,符合要求.
(4)如果充分利用北面旧墙,即矩形一边是50米旧墙时,用100米篱笆围成矩形仓库,则矩形另一边长为25米,这时矩形面积为S=50×25=1250(平方米).即面积可达1250平方米,符合设计要求.
还可以有其他一些符合要求的设计方案.请你试试看.
科目:初中数学 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:044
实践与探索课上,老师布置了这样一道题:
有100米长的篱笆材料,想围成一矩形露天仓库,要求面积不小于600平方米,在场地的北面有一堵长50米的旧墙.有人用这个篱笆围一个长40米,宽10米的矩形仓库,但面积只有400平方米,不合要求.现在请你设计矩形仓库的长和宽,使它符合要求.
经过同学们一天的实践与思考,老师收到了如下几种设计方案:
(1)如果设矩形的宽为x米,则用于长的篱笆为![]() =(50-x)米,这时面积S=x(50-x).
=(50-x)米,这时面积S=x(50-x).
当S=600时,由x(50-x)=600,得x2-50x+600=0,解得x1=20,x2=30.
检验后知x=20符合要求.
(2)根据在周长相等的条件下,正方形面积大于矩形面积,所以设计成正方形仓库,它的边长为x米,则4x=100,x=25.这时面积达到625米,当然符合要求.
(3)如果利用场地北面的那堵旧墙,取矩形的长与旧墙平行,设与墙垂直的矩形一边长为x米,则另一边为100-2x,如图.
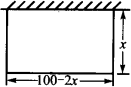
因为旧墙长50米,所以100-2x≤50.即x≥25米.若S=600平方米,则由x(100-2x)=600,即x2-50x+300=0,解得x1=25+![]() ,x2=25-
,x2=25-![]() .根据x≥25,舍去x2=25-
.根据x≥25,舍去x2=25-![]() .
.
所以,利用旧墙,取矩形垂直于旧墙一边长为25+![]() 米(约43米),另一边长约14米,符合要求.
米(约43米),另一边长约14米,符合要求.
(4)如果充分利用北面旧墙,即矩形一边是50米旧墙时,用100米篱笆围成矩形仓库,则矩形另一边长为25米,这时矩形面积为S=50×25=1250(平方米).即面积可达1250平方米,符合设计要求.
还可以有其他一些符合要求的设计方案.请你试试看.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com