
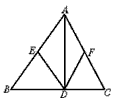
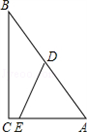
| 在△ABC中,AD⊥BC于D,E、F分别是AB、AC的中点,连结DE、DF,当△ABC满足条件AB=AC时,四边形AEDF是( ) |
|
A.矩形 B.菱形 C.平行四边形 D.正方形 |
科目:初中数学 来源: 题型:
科目:初中数学 来源:同步题 题型:填空题
科目:初中数学 来源: 题型:
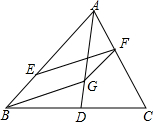 在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.| 9 | 4 |
科目:初中数学 来源: 题型:解答题
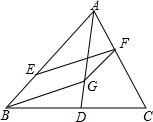 在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF.
在△ABC中,AD交BC于点D,E、F和G分别是边AB、AC和AD上的点,且BE=GF=AF,FG∥BE,连接BG,EF. ,试说明△ABG∽△AGF.
,试说明△ABG∽△AGF.科目:初中数学 来源:2012年福建省漳州市中考数学模拟试卷(二)(解析版) 题型:解答题
 ,试说明△ABG∽△AGF.
,试说明△ABG∽△AGF.
科目:初中数学 来源: 题型:
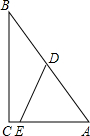 在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.
在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.科目:初中数学 来源:2011年上海市青浦区中考数学一模试卷(解析版) 题型:解答题
 ,点D是边AB上的一动点,过点D作DE∥BC,交边AC于点E
,点D是边AB上的一动点,过点D作DE∥BC,交边AC于点E
科目:初中数学 来源: 题型:解答题
 ,点D是边AB上的一动点,过点D作DE∥BC,交边AC于点E
,点D是边AB上的一动点,过点D作DE∥BC,交边AC于点E
科目:初中数学 来源: 题型:解答题
 在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.
在△ABC中,AC=6,BC=8,AB=10,点D、E分别在AB、AC上,且DE将△ABC的周长分成相等的两部分.设AE=x,AD=y,△ADE的面积为S.科目:初中数学 来源:四川省月考题 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com