
| 完成下面的证明. 已知:如图AB=CD,BE=CF,AF=DE. 求证:△ABE≌△DCF 证明:∵AF=DE(已知) ∴AF-EF=DE-EF(等式性质)即AE=DF 在△ABE和 △DCF中 ∵AB=CD , BE=CF(已知 ) AE=DF(已证) ∴△ABE≌△DCF( ) |
|
A.SSS B.SAS C.AAS |
科目:初中数学 来源: 题型:
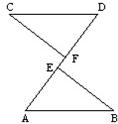 24、完成下面的证明.
24、完成下面的证明.科目:初中数学 来源:不详 题型:填空题

科目:初中数学 来源: 题型:填空题
 完成下面的证明.
完成下面的证明.科目:初中数学 来源:专项题 题型:填空题
科目:初中数学 来源: 题型:022
完成下面的证明.
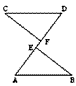
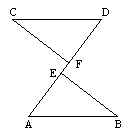
已知:如图AB=CD , BE=CF , AF=DE.求证:△ABE≌△DCF
证明:∵AF=DE(已知)
∴AF-EF=DE-EF( ) 即AE=DF
在△ABE和 △DCF中
∵AB=CD , BE=CF( )
AE=DF( )
∴△ABE≌△DCF( )
科目:初中数学 来源: 题型:解答题
完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )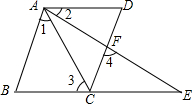
科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
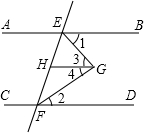 证明:∵HG∥AB(已知)
证明:∵HG∥AB(已知)| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源: 题型:
 12、完成下面的证明过程:
12、完成下面的证明过程:科目:初中数学 来源: 题型:
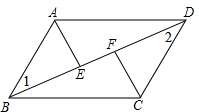 完成下面的证明过程
完成下面的证明过程 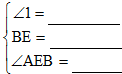
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com