
| 对于一组数据1,2,3,2,2,以下判断:①平均数为5;②中位数为2; ③众数为2; ④极差为2。正确的有 |
A.1个 B.2个 C.3个 D.4个 |
科目:初中数学 来源:期末题 题型:单选题
科目:初中数学 来源:湖南省中考真题 题型:单选题
科目:初中数学 来源: 题型:解答题
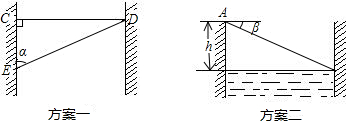
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 (单位:米) |
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 (单位:米) |
科目:初中数学 来源:不详 题型:解答题

| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 (单位:米) |
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 (单位:米) |
科目:初中数学 来源:2004年全国中考数学试题汇编《数据分析》(02)(解析版) 题型:解答题
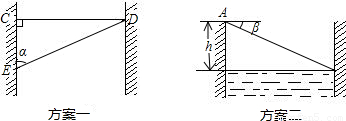
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 (单位:米) |
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 (单位:米) |
科目:初中数学 来源:2004年全国中考数学试题汇编《锐角三角函数》(06)(解析版) 题型:解答题

| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 (单位:米) |
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 (单位:米) |
科目:初中数学 来源:2004年四川省遂宁市中考数学试卷(解析版) 题型:解答题
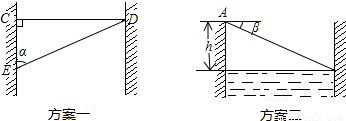
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 100 | 150 | 200 |
| α | 76°33′ | 71°35′ | 65°25′ |
| 计算得出河宽 (单位:米) |
| 测量次数 | 1 | 2 | 3 |
| EC(单位:米) | 14.4 | 13.8 | 12.5 |
| β | 1°24′ | 2°16′ | 1°56′ |
| 计算得出河宽 (单位:米) |
科目:初中数学 来源: 题型:

| 分组 | 频数 | 频率 | |
| 一组 | 0<t≤5 | 10 | 0.1 |
| 二组 | 5<t≤10 | 0.3 | |
| 三组 | 10<t≤15 | 25 | 0.25 |
| 四组 | 15<t≤20 | 20 | |
| 五组 | 20<t≤25 | 15 | 0.15 |
| 合计 | 1.00 | ||
| 所用时间t | 顾客满意程度 |
| 0<t≤10 | 比较满意 |
| 10<t≤15 | 基本满意 |
| t>15 | 比较差 |
科目:初中数学 来源: 题型:
工商银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).
下面是这次调查统计分析得到的频数分布表和频数分布直方图.
| 分组 | 频数 | 频率 | |
| 一组 | 0<t≤5 | 10 | 0.1 |
| 二组 | 5<t≤10 |
| 0.3 |
| 三组 | 10<t≤15 | 25 | 0.25 |
| 四组 | 15<t≤20 | 20 |
|
| 五组 | 20<t≤25 | 15 | 0.15 |
| 合计 |
| 1.00 |
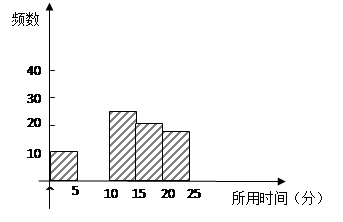 1.在上表中填写所缺数据
1.在上表中填写所缺数据
2.补全频数分布直方图
3.据调查顾客对服务质量的满意程度与所用时间t的关系如下:
| 所用时间t | 顾客满意程度 |
| 0<t≤10 | 比较满意 |
| 10<t≤15 | 基本满意 |
| t>15 | 比较差 |
请结合频数分布表和频数分布直方图回答:本次调查中,处于中位数的顾客对服务质量的满意程度为 ,顾客从开始排队到办理业务所用的时间平均为
分钟,用以上调查结果来判断工商银行全天的服务水平合理吗?为什么?
科目:初中数学 来源:2011-2012学年江苏省无锡市惠山区九年级5月模拟考试数学试卷(解析版) 题型:解答题
工商银行为改进在上下班高峰的服务水平,随机抽样调查了部分该行顾客在上下班高峰时从开始排队到办理业务所用的时间t(单位:分).
下面是这次调查统计分析得到的频数分布表和频数分布直方图.
|
分组 |
频数 |
频率 |
|
|
一组 |
0<t≤5 |
10 |
0.1 |
|
二组 |
5<t≤10 |
|
0.3 |
|
三组 |
10<t≤15 |
25 |
0.25 |
|
四组 |
15<t≤20 |
20 |
|
|
五组 |
20<t≤25 |
15 |
0.15 |
|
合计 |
|
1.00 |
 1.在上表中填写所缺数据
1.在上表中填写所缺数据
2.补全频数分布直方图
3.据调查顾客对服务质量的满意程度与所用时间t的关系如下:
|
所用时间t |
顾客满意程度 |
|
0<t≤10 |
比较满意 |
|
10<t≤15 |
基本满意 |
|
t>15 |
比较差 |
请结合频数分布表和频数分布直方图回答:本次调查中,处于中位数的顾客对服务质量的满意程度为 ,顾客从开始排队到办理业务所用的时间平均为
分钟,用以上调查结果来判断工商银行全天的服务水平合理吗?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com