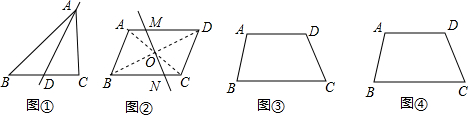
某班研究性学习小组在研究用一条直线等分几何图形的面积时,发现如下事实:
㈠如图①,对于三角形ABC,取BC边中点D,过A、D两点画一条直线即可.
理由:∵△ABD与△ADC等底等高,
∴S
△ABD=S
△ADC㈡如图②,对于平行四边形ABCD,连接两对角线AC、BD交于点O,过O点任作一直线MN即可.(不妨设与AD、BC分别交于点M、N)
理由:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC.∴∠MAO=∠NCO.
∴易得S
△AOM=S
△CON∴S
四边形ABNM=S
四边形CDMN.
受上面的启发,请你研究一下下面的问题:
某村王大爷家有一块梯形形状的稻田(如图③所示),已知:上底AD=40米,下底BC=60米,高h=30米,王大爷准备把这块梯形形状的稻田平均分给两个儿子(面积相等).
(1)分割方法有许多种,请你帮助王大爷设计两种不同的分割方案,在图③、图④中分别画出来,并说明理由;
(2)为了尽可能减少筑砌分割田坎的劳动量(只考虑田坎长度对工时的影响,不计其它因素),问:田坎应砌在什么位置最短?请画出图形,并求出此时分割线的长度.