
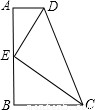
如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点, AD+BC=DC,下列结论中:①△ADE ∽△BEC;②DE2=DA·DC;③若设AD=a, CD=b,BC=c,则关于x的方程 有两个不相等的实数根; ④若设AD=a,AB=b,BC=c,则关于x的方程 有两个不相等的实数根; ④若设AD=a,AB=b,BC=c,则关于x的方程 有两个相等的实数根,其中正确的结论的个数有 有两个相等的实数根,其中正确的结论的个数有 |
|
A.1个 B.2个 C.3个 D.4个 |
科目:初中数学 来源: 题型:
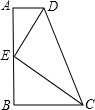 如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个.
如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个.| A、1个 | B、2个 | C、3个 | D、4个 |
科目:初中数学 来源: 题型:
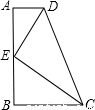
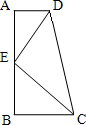 16、如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,AD+BC=CD,下列结论中:
16、如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,AD+BC=CD,下列结论中:科目:初中数学 来源:第2章《一元二次方程》好题集(08):2.3 公式法(解析版) 题型:选择题
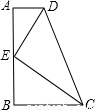
科目:初中数学 来源:第19章《相似形》好题集(22):19.6 相似三角形的性质(解析版) 题型:选择题
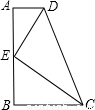
科目:初中数学 来源:第29章《相似形》好题集(18):29.5 相似三角形的性质(解析版) 题型:选择题
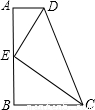
科目:初中数学 来源:第3章《图形的相似》好题集(17):3.3 相似三角形的性质和判定(解析版) 题型:选择题
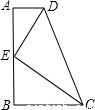
科目:初中数学 来源:第4章《一元二次方程》好题集(08):4.2 一元二次方程的解法(解析版) 题型:选择题
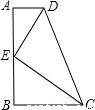
科目:初中数学 来源:第24章《图形的相似》好题集(20):24.3 相似三角形(解析版) 题型:选择题
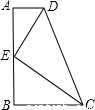
科目:初中数学 来源:第4章《相似三角形》好题集(18):4.3 两个三角形相似的判定(解析版) 题型:选择题
科目:初中数学 来源:第24章《相似形》好题集(17):24.3 相似三角形的性质(解析版) 题型:选择题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com