
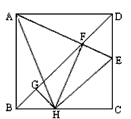
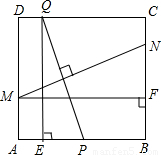
| 如图,在正方形ABCD中,AB=4,E为CD上一动点,连AE交BD于F,过F作FH⊥AE交BC于H,过H作 GH⊥BD交BD于G,下列有四个结论:(1)AF=FH,(2)∠HAE=45°,(3)BD=2FG,(4)△CEH的周长为定值,其中正确的结论是 |
|
A.⑴⑵⑶ B.⑴⑵⑷ C.⑴⑶⑷ D.⑴⑵⑶⑷ |
科目:初中数学 来源: 题型:
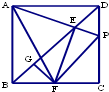 10、如图,在正方形ABCD中,AB=2,点P是CD上一动点,连接PA交BD于点E,过点E作EF⊥AP交BC于点F,过点F作FG⊥BD于点G,下列有四个结论:①AE=EF,②∠PAF=45°③BD=2EG,④△PCF的周长为定值,其中正确的结论是( )
10、如图,在正方形ABCD中,AB=2,点P是CD上一动点,连接PA交BD于点E,过点E作EF⊥AP交BC于点F,过点F作FG⊥BD于点G,下列有四个结论:①AE=EF,②∠PAF=45°③BD=2EG,④△PCF的周长为定值,其中正确的结论是( )科目:初中数学 来源: 题型:单选题
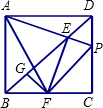 如图,在正方形ABCD中,AB=2,点P是CD上一动点,连接PA交BD于点E,过点E作EF⊥AP交BC于点F,过点F作FG⊥BD于点G,下列有四个结论:①AE=EF,②∠PAF=45°③BD=2EG,④△PCF的周长为定值,其中正确的结论是
如图,在正方形ABCD中,AB=2,点P是CD上一动点,连接PA交BD于点E,过点E作EF⊥AP交BC于点F,过点F作FG⊥BD于点G,下列有四个结论:①AE=EF,②∠PAF=45°③BD=2EG,④△PCF的周长为定值,其中正确的结论是科目:初中数学 来源:重庆市期中题 题型:单选题
科目:初中数学 来源: 题型:
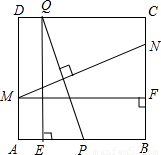
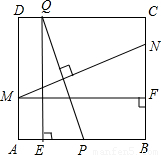
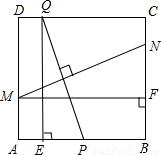
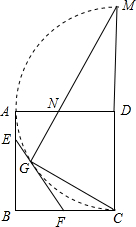
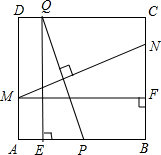 如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.科目:初中数学 来源:江苏中考真题 题型:解答题
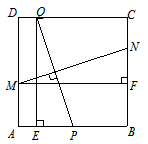
科目:初中数学 来源:2012年江苏省宿迁市钟吾中学中考数学模拟试卷(解析版) 题型:解答题
科目:初中数学 来源:2012年湖北省咸宁市中考数学模拟试卷(十三)(解析版) 题型:解答题
科目:初中数学 来源:2012年河北省中考数学模拟试卷(十一)(解析版) 题型:解答题
科目:初中数学 来源:2011年江苏省宿迁市中考数学试卷(解析版) 题型:解答题
科目:初中数学 来源: 题型:
 |
| AC |
 E作
E作 |
| AC |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com