如图,在平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标是(1,2)。将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线 上,则k的值为 上,则k的值为 |

|
A.2
B.3
C.4
D.6 |
相关习题
科目:初中数学
来源:吉林省期末题
题型:单选题
如图,在平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标是(1,2)。将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线
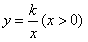
上,则k的值为
A.2
B.3
C.4
D.6
查看答案和解析>>
科目:初中数学
来源:
题型:
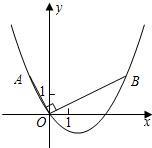
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:
题型:
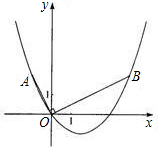
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
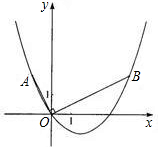 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式.
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(30):2.7 最大面积是多少(解析版)
题型:解答题
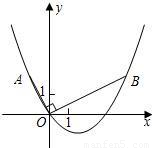
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:第34章《二次函数》中考题集(34):34.4 二次函数的应用(解析版)
题型:解答题
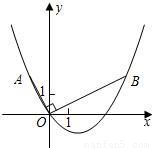
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版)
题型:解答题
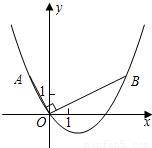
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:第6章《二次函数》中考题集(33):6.4 二次函数的应用(解析版)
题型:解答题
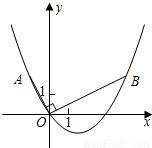
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:第27章《二次函数》中考题集(32):27.3 实践与探索(解析版)
题型:解答题
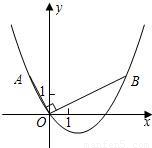
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>
科目:初中数学
来源:第26章《二次函数》中考题集(31):26.3 实际问题与二次函数(解析版)
题型:解答题
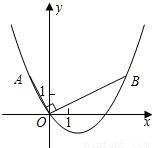
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上求出点P,使得S
△ABP=S
△ABO.
查看答案和解析>>

 上,则k的值为
上,则k的值为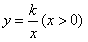 上,则k的值为
上,则k的值为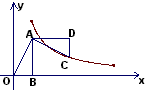
 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2)




