已知直线 与函数 与函数 的图象相交于点(a,b),则 的图象相交于点(a,b),则 的值是 的值是 |
A.13
B.11
C.7
D.5 |
相关习题
科目:初中数学
来源:福建省期末题
题型:单选题
已知直线
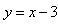
与函数
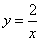
的图象相交于点(a,b),则
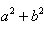
的值是
A.13
B.11
C.7
D.5
查看答案和解析>>
科目:初中数学
来源:
题型:
已知直线y=2x+4与x轴、y轴分别相交于A、C两点,抛物线y=ax2+bx+c(a≠0)经过点A、C和x轴上的另一点B(1,0).
(1)求抛物线的解析式,并画出函数图象略图;
(2)在直线AC上求点P,使以点A、B、P为顶点的三角形与△AOC相似;
(3)设抛物线的顶点为M,在抛物线上是否存在点Q,使△ABQ的面积等于△AMC面积的8倍?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
已知直线y=2x+4与x轴、y轴分别相交于A、C两点,抛物线y=ax2+bx+c(a≠0)经过点A、C和x轴上的另一点B(1,0).
(1)求抛物线的解析式,并画出函数图象略图;
(2)在直线AC上求点P,使以点A、B、P为顶点的三角形与△AOC相似;
(3)设抛物线的顶点为M,在抛物线上是否存在点Q,使△ABQ的面积等于△AMC面积的8倍?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
 已知:一次函数
已知:一次函数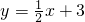 的图象与正比例函数y=kx的图象相交于点A(a,1).
的图象与正比例函数y=kx的图象相交于点A(a,1).
(1)求a的值及正比例函数y=kx的解析式;
(2)点P在坐标轴上(不与点O重合),若PA=OA,直接写出P点的坐标;
(3)直线x=m与一次函数的图象交于点B,与正比例函数图象交于点C,若△ABC的面积记为S,求S关于m的函数关系式(写出自变量的取值范围).
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
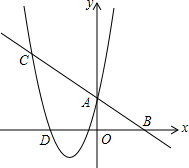 已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.
已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.
(1)当点C坐标为(-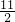 ,
,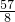 )时,求直线AB的解析式;
)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数y=x2-mx+3的图象上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数y=x2-mx+3有最小值-3,求实数m的值.
查看答案和解析>>
科目:初中数学
来源:2010-2011学年福建省泉州市德化五中九年级(上)第四次月考数学试卷(解析版)
题型:选择题
已知直线y=x-3与函数
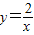
的图象相交于点(a,b),则a
2+b
2的值是( )
A.13
B.11
C.7
D.5
查看答案和解析>>
科目:初中数学
来源:2012年福建省泉州市南安市中考数学模拟试卷(三)(解析版)
题型:选择题
已知直线y=x-3与函数

的图象相交于点(a,b),则a
2+b
2的值是( )
A.13
B.11
C.7
D.5
查看答案和解析>>
科目:初中数学
来源:2012年福建省泉州市南安市中考数学模拟试卷(一)(解析版)
题型:选择题
已知直线y=x-3与函数
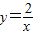
的图象相交于点(a,b),则a
2+b
2的值是( )
A.13
B.11
C.7
D.5
查看答案和解析>>
科目:初中数学
来源:2004年山西省临汾市中考数学试卷(解析版)
题型:解答题
已知直线y=2x+4与x轴、y轴分别相交于A、C两点,抛物线y=ax2+bx+c(a≠0)经过点A、C和x轴上的另一点B(1,0).
(1)求抛物线的解析式,并画出函数图象略图;
(2)在直线AC上求点P,使以点A、B、P为顶点的三角形与△AOC相似;
(3)设抛物线的顶点为M,在抛物线上是否存在点Q,使△ABQ的面积等于△AMC面积的8倍?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
已知反比例函数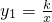 的图象与一次函数y2=kx+m的图象相交于A(2,1).
的图象与一次函数y2=kx+m的图象相交于A(2,1).
(1)分别求出这两个函数的解析式,并在同一坐标系内画出它们的大致图象;
(2)试判断P(-1,5)关于x轴的对称点Q是否在一次函数y2=kx+m的图象上,若在请求出S△APQ;若不在,请求出直线AQ的解析式;
(3)若一次函数的图象与反比例函数的图象的另一个交点为B,且B点的纵坐标为-4,请根据图象回答:①当x取何值时,y1>y2;②当x取何值时,y1•y2>0.
查看答案和解析>>

 已知:一次函数
已知:一次函数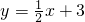 的图象与正比例函数y=kx的图象相交于点A(a,1).
的图象与正比例函数y=kx的图象相交于点A(a,1). 已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.
已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.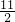 ,
,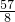 )时,求直线AB的解析式;
)时,求直线AB的解析式;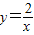 的图象相交于点(a,b),则a2+b2的值是( )
的图象相交于点(a,b),则a2+b2的值是( ) 的图象相交于点(a,b),则a2+b2的值是( )
的图象相交于点(a,b),则a2+b2的值是( )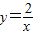 的图象相交于点(a,b),则a2+b2的值是( )
的图象相交于点(a,b),则a2+b2的值是( )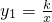 的图象与一次函数y2=kx+m的图象相交于A(2,1).
的图象与一次函数y2=kx+m的图象相交于A(2,1).