科目：初中数学 来源： 题型：

已知：如图，正方形ABCD中，CM=CD，MN⊥AC，连接CN，则∠DCN=

 

=

 

∠B，∠MNC=

 

=

 

∠B．

查看答案和解析>>

科目：初中数学 来源：2012年北师大版初中数学八年级上4.4矩形、正方形练习卷（解析版） 题型：填空题

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

查看答案和解析>>

科目：初中数学 来源：同步题 题型：填空题

已知：如图，正方形ABCD中，CM=CD，MN⊥AC，连结CN，则∠DCN=（    ）=（     ）∠B，∠MND=（     ）=（     ）∠B.

查看答案和解析>>

科目：初中数学 来源：101网校同步练习　初二数学　人教版(新课标2004年初审) 人教版(新课标2004年初审) 题型：047

已知：如图所示，正方形ABCD中，M为BC上任意一点，N是CD的中点，且AM＝DC＋CM．求证：AN平分∠DAM．

查看答案和解析>>

科目：初中数学 来源：数学教研室 题型：022

查看答案和解析>>

科目：初中数学 来源： 题型：

已知在正方形ABCD中，对角线AC、DB交于点O，E是CD边上一点，AE与对角线DB交于点M，连接CM．
（1）如图，点F是线段CB上一点，AF与DB交于点N，连接CN．若∠CME=30°，∠CNF=50°．求：∠EAF的度数；
（2）若点F′是CB延长线上一点，AF′与DB的延长线交于点N′，连接CN′．如果∠CME=α，∠CN′F′=β，请用含有α、β的代数式表示∠EAF′的度数：

90°+

α-β

2

90°+

α-β

2

．（第（2）问只需填写结论，不要求证明过程）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

查看答案和解析>>

科目：初中数学 来源： 题型：

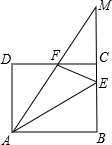如图，已知四边形ABCD是四个角都是直角，四条边都相等的正方形，点E在BC上，且CE=

1

4

BC，点F是CD的中点，延长AF与BC的延长线交于点M．以下结论：①AB=CM；②AE=AB+CE；③S_△AEF=

1

4

S四边形ABCF；④∠AFE=90°，其中正确的结论的个数有（　　）

A、1个

B、2个

C、3个

D、4个

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

如图，已知四边形ABCD是四个角都是直角，四条边都相等的正方形，点E在BC上，且CE=

1

4

BC，点F是CD的中点，延长AF与BC的延长线交于点M．以下结论：①AB=CM；②AE=AB+CE；③S_△AEF=

1

4

S四边形ABCF；④∠AFE=90°，其中正确的结论的个数有（　　）

A．1个

B．2个

C．3个

D．4个

查看答案和解析>>