
科目:初中数学 来源:福建省期末题 题型:解答题
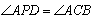 ,求点P的坐标;
,求点P的坐标;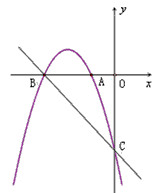
科目:初中数学 来源: 题型:
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 沿
沿![]() 轴向上平移3个单位长度后恰好经过
轴向上平移3个单位长度后恰好经过![]() 两点.
两点.
(1)求直线![]() 及抛物线的解析式;
及抛物线的解析式;
(2)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连结![]() ,求
,求![]() 与
与![]() 两角和的度数.
两角和的度数.
科目:初中数学 来源: 题型:
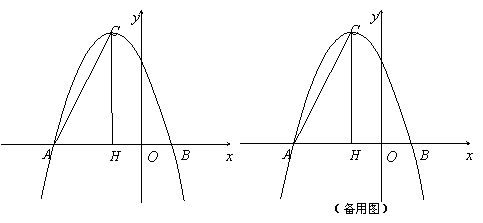
在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写:![]() = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在![]() 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
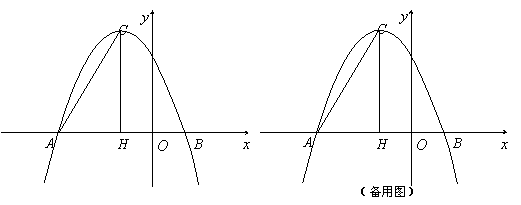 (3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
科目:初中数学 来源: 题型:
在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)根据题意求![]() ,b的值及顶点C的坐标;
,b的值及顶点C的坐标;
(2)在![]() 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
 |
科目:初中数学 来源: 题型:
在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与![]() 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线![]() 沿
沿![]() 轴向上平移3个单位长度后恰好经过B、C两点.
轴向上平移3个单位长度后恰好经过B、C两点.
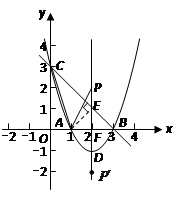
1.求直线BC及抛物线的解析式
2.设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
3.连结CD,求∠OCA与∠OCD两角度数的和
科目:初中数学 来源: 题型:
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与 y 轴交于点
的左侧),与 y 轴交于点![]() ,点
,点![]() 的坐标为(3,0),将直线 y=kx 沿 y 轴向上平移3个单位长度后恰好经过
的坐标为(3,0),将直线 y=kx 沿 y 轴向上平移3个单位长度后恰好经过 两点.
两点.
1.(1)求直线![]() 及抛物线的解析式;
及抛物线的解析式;
2.(2)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且 ,求点
,求点![]() 的坐标;
的坐标;
3.(3)连结![]() ,求
,求![]() 与
与![]() 两角和的度数.
两角和的度数.
科目:初中数学 来源: 题型:
 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿 轴向上平移3个单位长度后恰好经过B、C两点 .
轴向上平移3个单位长度后恰好经过B、C两点 .
科目:初中数学 来源:2012届江苏无锡北塘区中考二模数学试卷(带解析) 题型:解答题
在平面直角坐标系中,抛物线 与
与 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿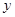 轴向上平移3个单位长度后恰好经过B、C两点 .
轴向上平移3个单位长度后恰好经过B、C两点 .
【小题1】求直线BC及抛物线的解析式
【小题2】设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
【小题3】连结CD,求∠OCA与∠OCD两角度数的和
科目:初中数学 来源:2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷9(带解析) 题型:解答题
在平面直角坐标系中,抛物线 与
与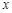 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写: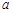 = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在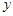 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 
科目:初中数学 来源:2012届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
在平面直角坐标系中,抛物线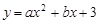 与
与 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点坐标;
(2)在 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 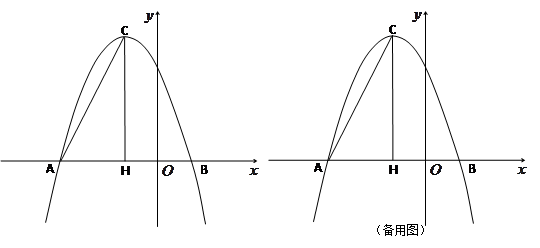
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com