
| 如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为 |
|
A.10° B.15° C.20° D.25° |
科目:初中数学 来源: 题型:
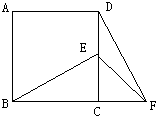 12、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )
12、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )科目:初中数学 来源: 题型:
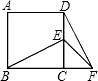 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为科目:初中数学 来源: 题型:
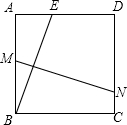 M,交DC于N.
M,交DC于N.科目:初中数学 来源: 题型:
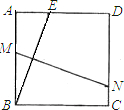 M,交DC于N,设AE=x.
M,交DC于N,设AE=x.科目:初中数学 来源: 题型:
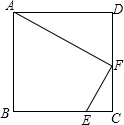 如图,在正方形ABCD中,边长为4a,F为DC的中点,E为BC上一点,且CE=
如图,在正方形ABCD中,边长为4a,F为DC的中点,E为BC上一点,且CE=| 1 | 4 |
科目:初中数学 来源: 题型:
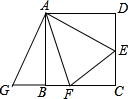 如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:科目:初中数学 来源: 题型:
 如图,在正方形ABCD中,E是DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF.若∠EFD=15°,则∠CDF的度数为( )
如图,在正方形ABCD中,E是DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF.若∠EFD=15°,则∠CDF的度数为( )科目:初中数学 来源: 题型:
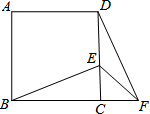
 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点; ,FC=
,FC=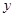 ,用含有
,用含有 的代数式来表示
的代数式来表示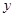 ,并写出
,并写出 的取值范围
的取值范围 ,如图2,当
,如图2,当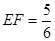 时,讨论△
时,讨论△ 与△
与△ 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.

科目:初中数学 来源:2012—2013学年山西农业大学附属中学八年级第一学期期中考数学卷(带解析) 题型:单选题
如图,在正方形ABCD中,E为DC边上的点,连接BE,将ΔBCE绕点C顺时针方向旋转90°得到ΔDCF,连接EF,若∠BEC=60°,则∠EFD的度数为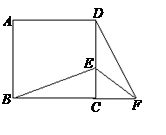
| A.10° | B.15° |
| C.20° | D.25° |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com