科目：初中数学 来源：同步题 题型：填空题

查看答案和解析>>

科目：初中数学 来源： 题型：

查看答案和解析>>

科目：初中数学 来源： 题型：

查看答案和解析>>

科目：初中数学 来源：江苏省无锡市天一实验学校2012届九年级一模数学试题 题型：044

在平面直角坐标系中，点B的坐标为(0，10)，点P、Q同时从O点出发，在线段OB上做往返运动，点P往返一次需10 s，点Q往返一次需6 s．设动点P、Q运动的时间为x( s)，动点离开原点的距离是y．

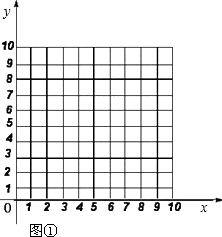
(1)当0≤x≤10时，在图①中，分别画出点P、点Q运动时关于x的函数图象，并回答：

①点P从O点出发，1个往返之间与点Q相遇几次(不包括O点)？

②点P从O点出发，几秒后与点Q第一次相遇？

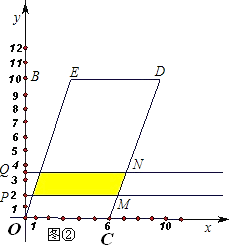
(2)如图②，在平面直角坐标系中，□OCDE的顶点C(6，0)，D、E、B在同一直线上．分别过点P、Q作PM、QN垂直于y轴，P、Q为垂足．设运动过程中两条直线PM，QN与□OCDE围成图形(阴影部分)的面积是S，试求当x(0≤x≤5)为多少秒时，S有最大值．最大值是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

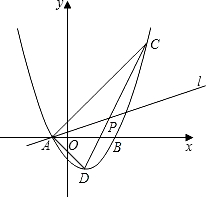如图，在平面直角坐标系中，开口向上的抛物线与x轴交于A、B两点，D为抛物线的顶点，O为坐标原点．若OA、OB（OA＜OB）的长分别是方程x²-4x+3=0的两根，且∠DAB=45°．
（1）求抛物线对应的二次函数解析式；
（2）过点A作AC⊥AD交抛物线于点C，求点C的坐标；
（3）在（2）的条件下，过点A任作直线l交线段CD于点P，若点C、D到直线l的距离分别记为d₁、d₂，试求的d₁+d₂的最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

查看答案和解析>>

科目：初中数学 来源：四川省中考真题 题型：解答题

如图，在平面直角坐标系中，开口向上的抛物线与x轴交于A、B两点，D为抛物线的顶点，O为坐标原点，若OA、OB（OA＜OB）的长分别是方程x²-4x+3=0的两根，且∠DAB=45°。
（1）求抛物线对应的二次函数解析式；
（2）过点A作AC⊥AD交抛物线于点C，求点C的坐标；
（3）在（2）的条件下，过点A任作直线l交线段CD于点P，若点C、D到直线l的距离分别记为d₁、d₂，试求的d₁+d₂的最大值。

查看答案和解析>>

科目：初中数学 来源：第34章《二次函数》中考题集（35）：34.4 二次函数的应用（解析版） 题型：解答题

如图，在平面直角坐标系中，开口向上的抛物线与x轴交于A、B两点，D为抛物线的顶点，O为坐标原点．若OA、OB（OA＜OB）的长分别是方程x²-4x+3=0的两根，且∠DAB=45°．
（1）求抛物线对应的二次函数解析式；
（2）过点A作AC⊥AD交抛物线于点C，求点C的坐标；
（3）在（2）的条件下，过点A任作直线l交线段CD于点P，若点C、D到直线l的距离分别记为d₁、d₂，试求的d₁+d₂的最大值．

查看答案和解析>>

科目：初中数学 来源：第6章《二次函数》中考题集（34）：6.4 二次函数的应用（解析版） 题型：解答题

如图，在平面直角坐标系中，开口向上的抛物线与x轴交于A、B两点，D为抛物线的顶点，O为坐标原点．若OA、OB（OA＜OB）的长分别是方程x²-4x+3=0的两根，且∠DAB=45°．
（1）求抛物线对应的二次函数解析式；
（2）过点A作AC⊥AD交抛物线于点C，求点C的坐标；
（3）在（2）的条件下，过点A任作直线l交线段CD于点P，若点C、D到直线l的距离分别记为d₁、d₂，试求的d₁+d₂的最大值．

查看答案和解析>>

科目：初中数学 来源：第27章《二次函数》中考题集（33）：27.3 实践与探索（解析版） 题型：解答题

如图，在平面直角坐标系中，开口向上的抛物线与x轴交于A、B两点，D为抛物线的顶点，O为坐标原点．若OA、OB（OA＜OB）的长分别是方程x²-4x+3=0的两根，且∠DAB=45°．
（1）求抛物线对应的二次函数解析式；
（2）过点A作AC⊥AD交抛物线于点C，求点C的坐标；
（3）在（2）的条件下，过点A任作直线l交线段CD于点P，若点C、D到直线l的距离分别记为d₁、d₂，试求的d₁+d₂的最大值．

查看答案和解析>>