
| 如图,△ABC内接于⊙O,连结OA、OB,若∠ABO=25°,则∠C的度数为 |
|
A.55° B.60° C.65° D.70° |
科目:初中数学 来源:2009年湖北省十堰市初中毕业生学业考试数学试题及答案 题型:013
如图,△ABC内接于⊙O,连结OA、OB,若∠ABO=25°,则∠C的度数为

A.55°
B.60°
C.65°
D.70°
科目:初中数学 来源: 题型:
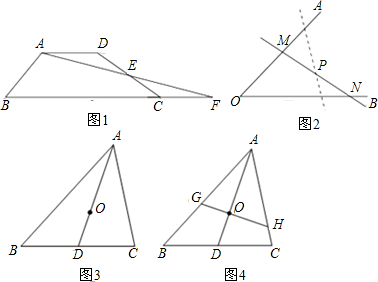
| AO |
| AD |
| 2 |
| 3 |
| S四边形BCHG |
| S△AGH |
科目:初中数学 来源: 题型:阅读理解
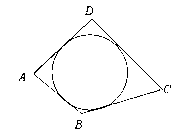
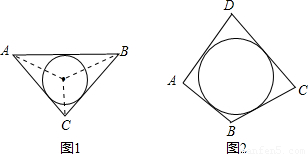
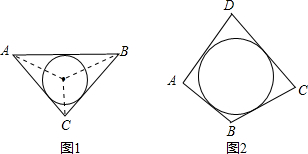 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
科目:初中数学 来源: 题型:解答题
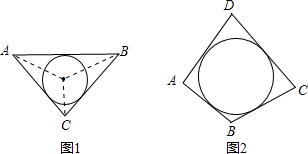 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA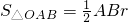 ,
,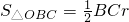 ,
,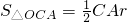
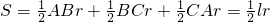
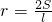
科目:初中数学 来源:河北省模拟题 题型:解答题
 ,
, ,
,



科目:初中数学 来源:2010年河北省廊坊市安次区中考数学一模试卷(解析版) 题型:解答题
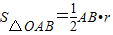 ,
,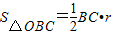 ,
,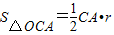
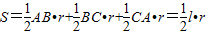
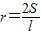
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com