| 平面内三点,可确定的直线的条数为 |
A.3
B.0或1
C.1或3
D.0 |
相关习题
科目:初中数学
来源:
题型:
平面内三点,可确定的直线的条数为( )
A.3 B.0或1 C.1或3 D.0
查看答案和解析>>
查看答案和解析>>
科目:初中数学
来源:1课1测七年级数学(上)
题型:022
经过平面内的三点A,B,C,可以确定直线的条数是________.
查看答案和解析>>
科目:初中数学
来源:
题型:
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.
(1)掷这样的立方体可能得到的点有哪些?请把这些点在如下给定的平面直角坐标系中表示出来;
(2)已知小明前两次掷得的两个点确定一条直线l,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线l上的概率是多少?
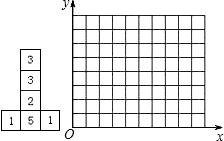
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.
(1)掷这样的立方体可能得到的点有哪些?请把这些点在如下给定的平面直角坐标系中表示出来;
(2)已知小明前两次掷得的两个点确定一条直线l,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线l上的概率是多少?
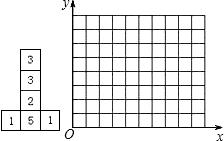
查看答案和解析>>
科目:初中数学
来源:不详
题型:解答题
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.
(1)掷这样的立方体可能得到的点有哪些?请把这些点在如下给定的平面直角坐标系中表示出来;
(2)已知小明前两次掷得的两个点确定一条直线l,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线l上的概率是多少?
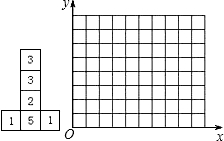
查看答案和解析>>
科目:初中数学
来源:《第25章 概率初步》2009年各小节同步练习(解析版)
题型:解答题
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内一个点的坐标.
(1)掷这样的立方体可能得到的点有哪些?请把这些点在如下给定的平面直角坐标系中表示出来;
(2)已知小明前两次掷得的两个点确定一条直线l,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线l上的概率是多少?
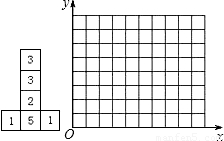
查看答案和解析>>
科目:初中数学
来源:
题型:阅读理解
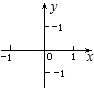
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是:
,∴m=
;已知点B(-2,n)在直线y=2x-1上,求n的方法是:
,∴n=
;
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先
,再由已知条件可得
.解得:
.∴满足已知条件的一次函数的解析式为:
.这个一次函数的图象与两坐标轴的交点坐标为:
,在右侧给定的平面直角坐标系中,描出这两个点,并画出这个函数的图象.像解决问题2这样,
的方法,叫做待定系数法.
查看答案和解析>>
科目:初中数学
来源:1999年全国中考数学试题汇编《一次函数》(02)(解析版)
题型:解答题
(1999•河北)九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是:______,∴m=______;已知点B(-2,n)在直线y=2x-1上,求n的方法是:______,∴n=______;
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先______,再由已知条件可得______
查看答案和解析>>
科目:初中数学
来源:1999年河北省中考数学试卷
题型:解答题
(1999•河北)九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
问题1:已知点A(m,1)在直线y=2x-1上,求m的方法是:
,∴m=
;已知点B(-2,n)在直线y=2x-1上,求n的方法是:
,∴n=
;
问题2:已知某个一次函数的图象经过点P(3,5)和Q(-4,-9),求这个一次函数的解析式时,一般先
,再由已知条件可得
.解得:
.∴满足已知条件的一次函数的解析式为:
.这个一次函数的图象与两坐标轴的交点坐标为:
,在右侧给定的平面直角坐标系中,描出这两个点,并画出这个函数的图象.像解决问题2这样,
的方法,叫做待定系数法.
查看答案和解析>>





 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
