练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA=PB，则必须添加的条件是（    ）。


    A.OA=OB
    B.PA⊥OA于A
    C.PB⊥OB于B
    D.PA⊥OA于A，PB⊥OB于B
    D
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：同步题 题型：填空题

    如图，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA=PB，则必须添加的条件是（    ）。

    查看答案和解析>>

    科目：初中数学 来源：设计八年级上数学人教版 人教版 题型：022

    如图，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA＝PB，则必须添加的条件是________．

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市青春中学2012届九年级中考模拟数学试题 题型：044

    如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的△AOB，△COD处，直角边OB，OD在x轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至△PEF处时，设PE．PF与OC分别交于点M，N，与x轴分别交于点G，H．

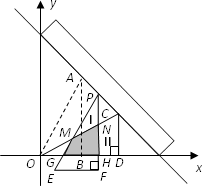
    (1)求直线AC所对应的函数关系式；

    (2)当点P是线段AC(端点除外)上的动点时，试探究：

    ①点M到x轴的距离h与线段BH的长是否总相等？请说明理由；

    ②两块纸板重叠部分(图中的阴影部分)的面积S是否存在最大值？若存在，求出这个最大值及S取最大值时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2008年江苏省连云港市初中毕业升学统一考试、数学试卷 题型：044

    如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的△AOB，△COD处，直角边OB，OD在x轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至△PEF处时，设PE，PF与OC分别交于点M，N，与x轴分别交于点G，H．

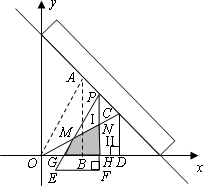
    (1)求直线AC所对应的函数关系式；

    (2)当点P是线段AC(端点除外)上的动点时，试探究：

    ①点M到x轴的距离h与线段BH的长是否总相等？请说明理由；

    ②两块纸板重叠部分(图中的阴影部分)的面积S是否存在最大值？若存在，求出这个最大值及S取最大值时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：填空题

    如图所示，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA=PB，则必须添加的条件是（    ）。

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    如图13-3-13，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA＝PB，则必须添加的条件是________.

    　　　　

    图13-3-13　　　　　　　　

    　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    如图13-3-5，若点P在∠AOB的平分线上，若应用角平分线的性质可得PA＝PB，则必须添加的条件是___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，平面直角坐标系xOy中，A(2
    		3
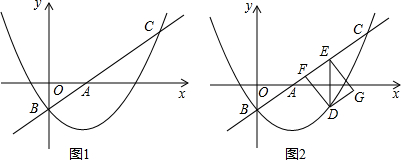
    ，2)    ，B（4，0）．将△OAB绕点O顺时针旋转a角（0°＜a＜90°）得到△OCD（O，A，B的对应点分别为O，C，D），将△OAB沿x轴负方精英家教网向平移m个单位得到△EFG（m＞0，O，A，B的对应点分别为E，F，G），a，m的值恰使点C，D，F落在同一反比例函数y=
    k
    x
    （k≠0）的图象上．
    （1）∠AOB=
     
    °，a=
     
    °；
    （2）求经过点A，B，F的抛物线的解析式；
    （3）若（2）中抛物线的顶点为M，抛物线与直线EF的另一个交点为H，抛物线上的点P满足以P，M，F，A为顶点的四边形的面积与四边形MFAH的面积相等（点P不与点H重合），请直接写出满足条件的点P的个数，并求位于直线EF上方的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•团风县模拟）如图1，在平面直角坐标系xOy中，直线l：y=
    3
    4
    x+m    与x轴、y轴分别交于点A和点B（0，-1），抛物线y=
    1
    2
    x2+bx+c    经过点B，且与直线l的另一个交点为C（4，n）．

    （1）求n的值和抛物线的解析式；
    （2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
    （3）M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    探究与应用：在学习几何时，我们可以通过分离和构造基本图形，将几何“模块”化．例如在相似三角形中，K字形是非常重要的基本图形，可以建立如下的“模块”（如图①）：
    （1）请就图①证明上述“模块”的合理性．已知：∠A=∠D=∠BCE=90°，求证：△ABC∽△DCE；
    （2）请直接利用上述“模块”的结论解决下面两个问题：
    ①如图②，已知点A（-2，1），点B在直线y=-2x+3上运动，若∠AOB=90°，求此时点B的坐标；
    ②如图③，过点A（-2，1）作x轴与y轴的平行线，交直线y=-2x+3于点C、D，求点A关于直线CD的对称点E的坐标．

    查看答案和解析>>


    同步练习册答案