练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    等边三角形每边上的中线、角平分线、高重合且相等

    A.正确
    B.错误
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：同步题 题型：填空题

    等边三角形每边上的中线、角平分线、高（    ）且（    ）。

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    等边三角形每边上的中线、角平分线、高________且________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    等边三角形的性质
    （1）等边三角形的三个内角都
    相等
    相等
    ，并且每一个角都等于
    60°
    60°
    ．
    （2）等边三角形是轴对称图形，共有
    三
    三
    条对称轴．
    （3）等边三角形每边上的
    中线
    中线
    、
    高线
    高线
    和该边所对内角的平分线互相重合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

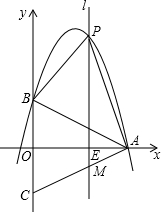    如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-数学公式x2+数学公式x+4经过A、B两点．
    （1）写出点A、点B的坐标；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；
    （3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013年山东省泰安市中考数学模拟试卷（八）（解析版） 题型：解答题

    如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-x2+x+4经过A、B两点．
    （1）写出点A、点B的坐标；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；
    （3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

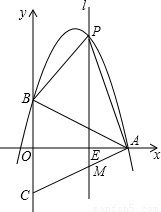
    科目：初中数学 来源：2013年浙江省杭州市锦绣?育才教育集团中考数学一模试卷（解析版） 题型：解答题

    如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-x2+x+4经过A、B两点．
    （1）写出点A、点B的坐标；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；
    （3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012年广西河池市中考数学试卷（解析版） 题型：解答题

    如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-x2+x+4经过A、B两点．
    （1）写出点A、点B的坐标；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；
    （3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

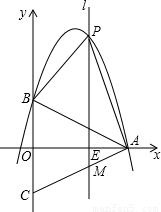
    科目：初中数学 来源： 题型：

    （2012•天津）“三等分任意角”是数学史上一个著名问题．已知一个角∠MAN，设∠α=
    13
    ∠MAN．
    （Ⅰ）当∠MAN=69°时，∠α的大小为
    23
    23
    （度）；
    （Ⅱ）如图，将∠MAN放置在每个小正方形的边长为1cm的网格中，角的一边AM与水平方向的网格线平行，另一边AN经过格点B，且AB=2.5cm．现要求只能使用带刻度的直尺，请你在图中作出∠α，并简要说明做法（不要求证明）
    如图，让直尺有刻度一边过点A，设该边与过点B的竖直方向的网格线交于点C，与过点B水平方向的网格线交于点D，保持直尺有刻度的一边过点A，调整点C、D的位置，使CD=5cm，画射线AD，此时∠MAD即为所求的∠α．
    如图，让直尺有刻度一边过点A，设该边与过点B的竖直方向的网格线交于点C，与过点B水平方向的网格线交于点D，保持直尺有刻度的一边过点A，调整点C、D的位置，使CD=5cm，画射线AD，此时∠MAD即为所求的∠α．
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

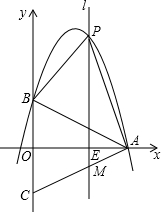    （2012•河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-
    1
    2
    x2+
    7
    2
    x+4经过A、B两点．
    （1）写出点A、点B的坐标；
    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；
    （3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（浙江宁波卷）数学（解析版） 题型：解答题

    若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．

    （1）如图1，在梯形ABCD中，AD∥BC，∠BAD=120°，∠C=75°，BD平分∠ABC．求证：BD是梯形ABCD的和谐线；

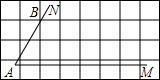
    （2）如图2，在12×16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；

    （3）四边形ABCD中，AB=AD=BC，∠BAD=90°，AC是四边形ABCD的和谐线，求∠BCD的度数．

     

    查看答案和解析>>


    同步练习册答案