
| 如图所示,△ABC绕点A顺时针旋转60°至△ADE位置,如果∠BAC=120°,连结BD、CE,则△BAD与 △ACE是( )三角形 |
|
A.直角 B.等边 C.等腰 D.等腰直角 |
科目:初中数学 来源:专项题 题型:解答题
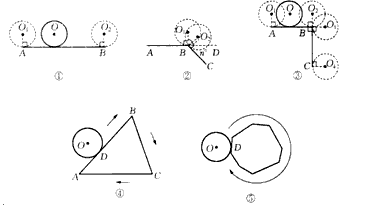
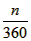 周。
周。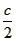 ,⊙O从⊙O1的位置出发, 在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转了____周。
,⊙O从⊙O1的位置出发, 在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转了____周。科目:初中数学 来源: 题型:
 22、一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行.
22、一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行.
科目:初中数学 来源: 题型:
Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板,按如图①所示拼在一起,CB与DE重合.
(1)试说明:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时针方向旋转到如图②中△A'B'C'位置,直线B'C'与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并说明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少![]() 度时
度时![]() ,四边形PCQB为菱形(不要求说理).
,四边形PCQB为菱形(不要求说理).
科目:初中数学 来源: 题型:044
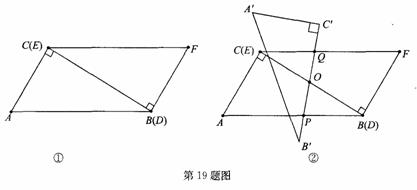
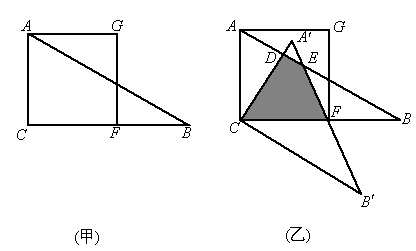
如图,把正方形ACFG与Rt△ACB按如图(甲)所示重叠在一起,其中AC=2,∠BAC=60°,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得△A′B′C′,AB分别与A′C、A′B′相交于点D、E,如图(乙)所示。
(1)、△ABC至少旋转多少度才能得到△A′B′C′?说明理由;
(2)、求△ABC与△A′B′C′重叠部分(即四边形CDEF)的面积。(若取近似值,则精确到0.1)
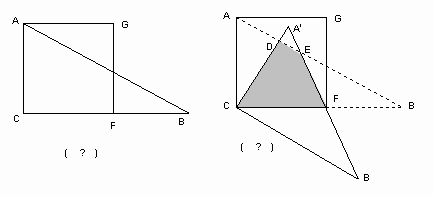
科目:初中数学 来源:四川省遂宁市2006年初中毕业暨高中阶段学校招生统一考试数学试题 题型:044
如图,把正方形ACFG与Rt△ACB按如图(甲)所示重叠在一起,其中AC=2,∠BAC=60°,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得![]() ,AB分别与
,AB分别与![]() 相交于点D、E,如图(乙)所示.
相交于点D、E,如图(乙)所示.

(1)、△ABC至少旋转多少度才能得到![]() ?说明理由;
?说明理由;
(2)、求△ABC与![]() 重叠部分(即四边形CDEF)的面积.(若取近似值,则精确到0.1)
重叠部分(即四边形CDEF)的面积.(若取近似值,则精确到0.1)
科目:初中数学 来源: 题型:044
(2006,遂宁)如图,把正方形ACFG与Rt△ACB按如图(甲)所示重叠在一起,其中AC=2,∠BAC=60°,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得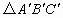 ,AB分别与
,AB分别与 、
、 相交于点D、E,如图(乙)所示.
相交于点D、E,如图(乙)所示.
(1)△ABC至少旋转多少度才能得到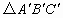 ?说明理由;
?说明理由;
(2)求△ABC与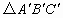 重叠部分(即四边形CDEF)的面积.(若取近似值,则精确到0.1)
重叠部分(即四边形CDEF)的面积.(若取近似值,则精确到0.1)
科目:初中数学 来源: 题型:
已知等边△ABC和Rt△DEF按如图所示的位置放置,点B,D重合,且点E、B(D)、
C在同一条直线上.其中∠E=90°, ![]() ,
,![]() ,现将△DEF
,现将△DEF
沿直线BC以每秒![]() 个单位向右平移,直至E点与C 点重合时停止运动,设运动时
个单位向右平移,直至E点与C 点重合时停止运动,设运动时
间为t秒.
(1) 试求出在平移过程中,点F落在△ABC的边上时的t值;
(2) 试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式;
(3) 当D与C重合时,点H为直线DF上一动点,现将△DBH绕点D顺时针旋转60°得到
△ACK,则是否存在点H使得△BHK的面积为![]() ,若存在,试求出CH的值;若不存在,请说明理由.
,若存在,试求出CH的值;若不存在,请说明理由.


科目:初中数学 来源: 题型:
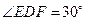 ,
, ,现将△DEF
,现将△DEF 个单位向右平移,直至E点与C 点重合时停止运动,设运动时
个单位向右平移,直至E点与C 点重合时停止运动,设运动时 ,若存在,试求出CH的值;若不存在,请说明理由.
,若存在,试求出CH的值;若不存在,请说明理由.

科目:初中数学 来源:2011-2012年重庆一中初三上学期期中考试数学卷 题型:解答题
已知等边△ABC和Rt△DEF按如图所示的位置放置,点B,D重合,且点E、B(D)、
C在同一条直线上.其中∠E=90°,  ,
,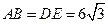 ,现将△DEF
,现将△DEF
沿直线BC以每秒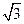 个单位向右平移,直至E点与C 点重合时停止运动,设运动时
个单位向右平移,直至E点与C 点重合时停止运动,设运动时
间为t秒.
(1) 试求出在平移过程中,点F落在△ABC的边上时的t值;
(2) 试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式;
(3) 当D与C重合时,点H为直线DF上一动点,现将△DBH绕点D顺时针旋转60°得到
△ACK,则是否存在点H使得△BHK的面积为 ,若存在,试求出CH的值;若不存在,请说明理由.
,若存在,试求出CH的值;若不存在,请说明理由.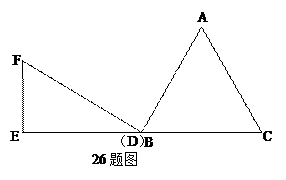

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com