练习册

  • 练习册
  • 试题
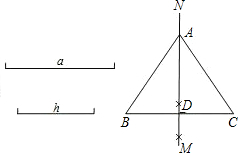
    精英家教网 > 初中数学 > 题目详情
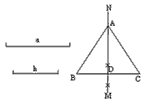
    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h。张红的作法是：（1）作线段BC=a；（2）作线段BC的垂直平分线MN，MN与BC相交于点D；（3）在直线MN上截取线段h；（4）连结AB，AC，△ABC为所求的等腰三角形。上述作法的四个步骤中，有错误的一步你认为是


    A.（1）
    B.（2）
    C.（3）
    D.（4）
    C
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    9、如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：
    （1）作线段BC=a；
    （2）作线段BC的垂直平分线MN，MN与BC相交于点D；
    （3）在直线MN上截取线段h；
    （4）连接AB，AC，△ABC为所求的等腰三角形．
    上述作法的四个步骤中，有错误的一步你认为是（　　）

    查看答案和解析>>

    科目：初中数学 来源：益阳 题型：单选题

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：
    （1）作线段BC=a；
    （2）作线段BC的垂直平分线MN，MN与BC相交于点D；
    （3）在直线MN上截取线段h；
    （4）连接AB，AC，△ABC为所求的等腰三角形．
    上述作法的四个步骤中，有错误的一步你认为是（　　）
    A．（1）B．（2）C．（3）D．（4）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年新人教版九年级（上）期末复习检测数学试卷（七）（解析版） 题型：选择题

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：
    （1）作线段BC=a；
    （2）作线段BC的垂直平分线MN，MN与BC相交于点D；
    （3）在直线MN上截取线段h；
    （4）连接AB，AC，△ABC为所求的等腰三角形．
    上述作法的四个步骤中，有错误的一步你认为是（ ）

    A．（1）
    B．（2）
    C．（3）
    D．（4）

    查看答案和解析>>

    科目：初中数学 来源：《第1章 证明（二）》2009年水平测试A卷（解析版） 题型：选择题

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：
    （1）作线段BC=a；
    （2）作线段BC的垂直平分线MN，MN与BC相交于点D；
    （3）在直线MN上截取线段h；
    （4）连接AB，AC，△ABC为所求的等腰三角形．
    上述作法的四个步骤中，有错误的一步你认为是（ ）

    A．（1）
    B．（2）
    C．（3）
    D．（4）

    查看答案和解析>>

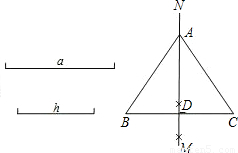
    科目：初中数学 来源： 题型：单选题

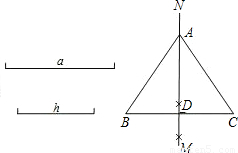
    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h．张红的作法是：
    （1）作线段BC=a；
    （2）作线段BC的垂直平分线MN，MN与BC相交于点D；
    （3）在直线MN上截取线段h；
    （4）连接AB，AC，△ABC为所求的等腰三角形．
    上述作法的四个步骤中，有错误的一步你认为是


    1. A.
      （1）
    2. B.
      （2）
    3. C.
      （3）
    4. D.
      （4）

    查看答案和解析>>

    科目：初中数学 来源：湖南省中考真题 题型：单选题

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h。张红的作法是：（1）作线段BC=a；（2）作线段BC的垂直平分线MN，MN与BC相交于点D；（3）在直线MN上截取线段h；（4）连结AB，AC，△ABC为所求的等腰三角形。上述作法的四个步骤中，有错误的一步你认为是

    [     ]

    A、（1）
    B、（2）
    C、（3）
    D、（4）

    查看答案和解析>>

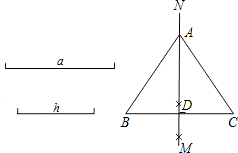
    科目：初中数学 来源：同步题 题型：单选题

    如图，已知线段a，h作等腰△ABC，使AB=AC，且BC=a，BC边上的高AD=h。张红的作法是：（1）作线段BC=a；（2）作线段BC的垂直平分线MN，MN与BC相交于点D；（3）在直线MN上截取线段h；（4）连结AB，AC，△ABC为所求的等腰三角形。上述作法的四个步骤中，有错误的一步你认为是
    [     ]
    A.（1）
    B.（2）
    C.（3）
    D.（4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：013

    如图，已知线段a，h作等腰△ABC，使AB＝AC，且BC＝a，BC边上的高AD＝h. 张红的作法是：（1）作线段BC＝a；（2）作线段BC的垂直平分线MN，MN与BC相交于点D；（3）在直线MN上截取线段h；（4）连结AB，AC，△ABC为所求的等腰三角形. 上述作法的四个步骤中，有错误的一步你认为是

    A．(1）　　B．(2）　　C．(3）　　D．(4）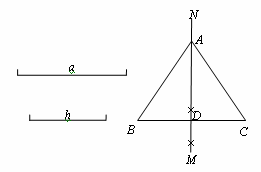

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知：△ABC为边长是4
    		3
    的等边三角形，四边形DEFG为边长是6的正方形．现将等边△ABC和正方形DEFG按如图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，△ABC从图1的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点C与点F重合时暂停运动，设△ABC的运动时间为t秒（t≥0）．

    （1）在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，请直接写出S与t之间的函数关系式；
    （2）如图2，当点A与点D重合时，作∠ABE的角平分线BM交AE于M点，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN．在线段AG上是否存在H点，使得△ANH为等腰三角形．如果存在，请求出线段EH的长度；若不存在，请说明理由．
    （3）如图3，若四边形DEFG为边长为4
    		3
    的正方形，△ABC的移动速度为每秒
    		3
    个单位长度，其余条件保持不变．△ABC开始移动的同时，Q点从F点开始，沿折线FG-GD以每秒2
    		3
    个单位长度开始移动，△ABC停止运动时，Q点也停止运动．设在运动过程中，DE交折线BA-AC于P点，则是否存在t的值，使得PC⊥EQ，若存在，请求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知直线y=-
    34
    x+3与x轴、y轴分别交于点A、B，线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°．
    （1）求△AOB的面积；
    （2）求点C坐标；
    （3）点P是x轴上的一个动点，设P（x，0），
    ①请用x的代数式表示PB2、PC2；
    ②是否存在这样的点P，使得|PC-PB|的值最大？如果不存在，请说明理由；如果存在，请直接写出点P的坐标
    （-21，0）
    （-21，0）
    ．

    查看答案和解析>>


    同步练习册答案