
| 已知:如图,B、C是线段AD上两点,且AB∶BC∶CD=2∶4∶3,M是AD的中点,CD=6㎝,线段MC=( )cm |
|
A.3 B.6 C.9 D.12 |
科目:初中数学 来源:中考数学专项练习 题型:044
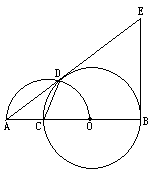
已知:如图,O是线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E,连结CD,若AC=2,且AC、AD的长是关于x的方程![]() -kx+
-kx+![]() =0的两个根.
=0的两个根.
(1)证明:AE切⊙O于点D;
(2)求线段EB的长;
(3)求tan∠ADC的值.
科目:初中数学 来源: 题型:
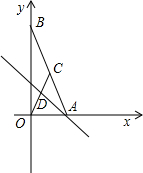 已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD.
已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD.科目:初中数学 来源: 题型:解答题
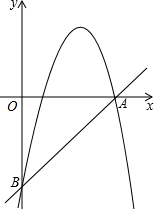 已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线
已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线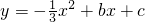 经过A、B两点.
经过A、B两点.科目:初中数学 来源: 题型:解答题
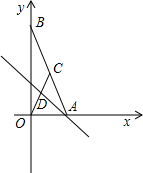 已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD.
已知:如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,且OD=2CD.科目:初中数学 来源:2012年上海市闸北区中考数学一模试卷(解析版) 题型:解答题
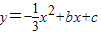 经过A、B两点.
经过A、B两点.
科目:初中数学 来源: 题型:
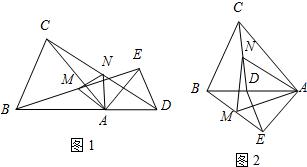 24、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
24、已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.科目:初中数学 来源: 题型:解答题
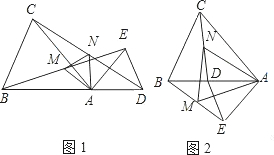 E,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
E,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.科目:初中数学 来源: 题型:
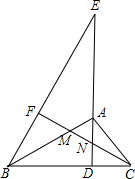 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.| 5 |
| 4 |
| 15 |
| 8 |
| 9 |
| 8 |
科目:初中数学 来源: 题型:
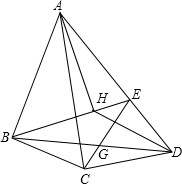 如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设
如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设| BG |
| GD |
| DE |
| EA |
| 3 | 7k2+20 |
| BH |
| HE |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com