
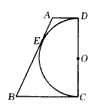
| 如图所示,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D、C、E若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是 |
|
A.9 B.10 C.12 D.14 |
科目:初中数学 来源:专项题 题型:单选题
科目:初中数学 来源: 题型:
 x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.科目:初中数学 来源: 题型:解答题
 x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.科目:初中数学 来源: 题型:
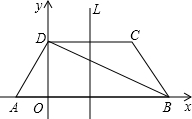
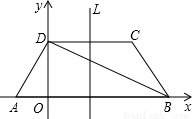
如图所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为![]() 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使![]() PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)

科目:初中数学 来源: 题型:
如图所示,在梯形ABCD中,已知AB∥DC, AD⊥DB,AD=DC=CB,
AB=4.以AB所在直线为![]() 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.

1.(1)求∠DAB的度数及A、D、C三点的坐标;
2.(2)求过A、D、C三点的抛物线的解析式及其
对称轴L.
3.(3)若P是抛物线的对称轴L上的点,那么使
![]() PDB为等腰三角形的点P有几个?
PDB为等腰三角形的点P有几个?
(不必求点P的坐标,只需说出个数即可)
科目:初中数学 来源: 题型:
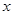 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为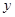 轴建立平面直角坐标系.
轴建立平面直角坐标系.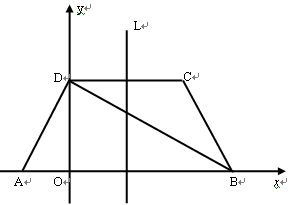
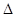 PDB为等腰三角形的点P有几个?
PDB为等腰三角形的点P有几个?科目:初中数学 来源:2011年广东省汕头市潮南区中考模拟考试数学卷 题型:解答题
如图所示,在梯形ABCD中,已知AB∥DC, AD⊥DB,AD=DC=CB,
AB=4.以AB所在直线为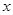 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为 轴建立平面直角坐标系.
轴建立平面直角坐标系.
【小题1】(1)求∠DAB的度数及A、D、C三点的坐标;
【小题2】(2)求过A、D、C三点的抛物线的解析式及其
对称轴L.
【小题3】(3)若P是抛物线的对称轴L上的点,那么使 PDB为等腰三角形的点P有几个?
PDB为等腰三角形的点P有几个?
(不必求点P的坐标,只需说出个数即可)
科目:初中数学 来源:第2章《二次函数》中考题集(35):2.7 最大面积是多少(解析版) 题型:解答题

科目:初中数学 来源:第34章《二次函数》中考题集(38):34.4 二次函数的应用(解析版) 题型:解答题
科目:初中数学 来源:第6章《二次函数》中考题集(38):6.4 二次函数的应用(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com