
| P是∠MON的平分线OC上一点,A是射线OM上一点,B是射线ON上一点,图中线段PA和PB一定相等的是 |
A.  B.  C.  D.  |
科目:初中数学 来源: 题型:

科目:初中数学 来源:2011届辽宁省丹东七中九年级中考一模数学试题(带解析) 题型:解答题
、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
【小题1】点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.
【小题2】点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?
【小题3】若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.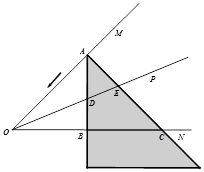
科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
 王老师布置学生用刻度尺画已知∠MON的平分线.小勇的画法是:
王老师布置学生用刻度尺画已知∠MON的平分线.小勇的画法是:科目:初中数学 来源: 题型:
王老师布置学生用刻度尺画已知∠MON的平分线。
小勇的画法是:1、在射线OM和ON上分别任取OA=OB,
2、连接AB,取AB的中点C,
3、作射线OC,
则射线OC就是∠MON的平分线。
小聪的画法是:1、在射线OM上任取A、C两点,
2、在射线ON上截取OB=OA,OD=OC
3、连接AD和BC ,AD和BC交于点P
4、作射线OP
则射线OP就是∠MON的平分线。
请你选择一种画法在右图中画出相应的图形,然后给予证明
 |
科目:初中数学 来源: 题型:
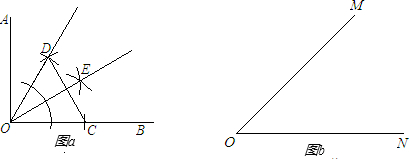
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 3 |
科目:初中数学 来源:江苏模拟题 题型:解答题
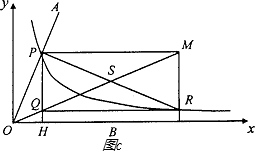
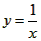 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R, 分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R, 分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=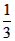 ∠AOB,要明白帕普斯的方法,请研究以下问题:
∠AOB,要明白帕普斯的方法,请研究以下问题: 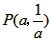 、
、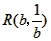 ,求直线OM对应的函数关系式(用含a、b的代数式表示);
,求直线OM对应的函数关系式(用含a、b的代数式表示);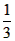 ∠AOB。
∠AOB。
科目:初中数学 来源:辽宁省铁岭市2010年中考数学试题 题型:059
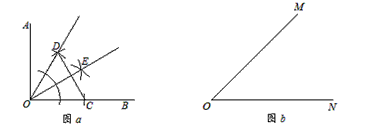
如图,一个直角三角形纸片的顶点
A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
(1)
点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.(2)
点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?(3)
若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.科目:初中数学 来源: 题型:
 23、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
23、如图,一个直角三角形纸片的顶点A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com