
| 分别用x和y表示等腰三角形的顶角和底角,则y与x的函数关系式为( ) A.y=90-x B.y=2x C.y=90-  x xD.y=180-  x x |
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:数学教研室 题型:044
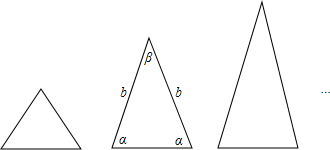
设三角形的底和腰分别为a和b,底角和顶角分别为![]() 、
、![]() ,要求“正度”值是非负数。
,要求“正度”值是非负数。
同学甲认为:可用式子![]() 表示“正度”,
表示“正度”,![]() 的值越小,表示等腰三角形越接近于正三角形。
的值越小,表示等腰三角形越接近于正三角形。
探究:(1)他们的方案哪个较合理,为什么?
(2)请再给出一个衡量“正度”的表达式。
科目:初中数学 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:044
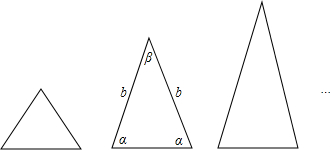
如图,这些等腰三角形与正三角形的形状有差异,我们把它与正三角形的接近程度称为“正度”.在研究“正度”时,应保证相似三角形的“正度”相等.

设等腰三角形的底和腰分别为a、b,底角和顶角分别为α、β,要求“正度”的值是非负数.
同学甲认为:可用式子|a-b|来表示“正度”,|a-b|的值越小,表示的等腰三角形越接近正三角形;
同学乙认为:可用式子|α-β|来表示“正度”,|α-β|的值越小,表示的等腰三角形越接近正三角形.
探究:(1)他们的方案哪个较为合理,为什么?
(2)对你认为不够合理的方案,请加以改进(给出式子即可);
(3)请再给出一种衡量“正度”的表达式.
科目:初中数学 来源: 题型:
科目:初中数学 来源:《27.2 相似三角形》2009年同步练习(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com