
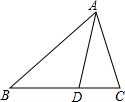
| 如图,在△ABC中,AD是△ABC中∠BAC的平分线,且BD>DC,则下列说法中正确的是 |
|
A、点D到AB边的距离大于点D到AC边的距离 B、点D到AB边的距离小于点D到AC边的距离 C、点D到AB边的距离等于点D到AC边的距离 D、点D到AB边的距离与点D到AC边的距离大小关系不确定 |
科目:初中数学 来源:不详 题型:单选题
| A.点D到AB边的距离大于点D到AC边的距离 |
| B.点D到AB边的距离小于点D到AC边的距离 |
| C.点D到AB边的距离等于点D到AC边的距离 |
| D.点D到AB边的距离与点D到AC边的距离大小关系不确定 |
科目:初中数学 来源: 题型:单选题
 如图,在△ABC中,AD是△ABC中∠BAC的平分线,且BD>DC,则下列说法中正确的是
如图,在△ABC中,AD是△ABC中∠BAC的平分线,且BD>DC,则下列说法中正确的是科目:初中数学 来源:期末题 题型:单选题

[ ]
科目:初中数学 来源:江苏省泰州市海陵区2010-2011学年度八年级第一学期期末考试数学试题 题型:013
如图,在△ABC中,AD是△ABC中∠BAC的平分线,且BD>DC,则下列说法中正确的是

点D到AB边的距离大于点D到AC边的距离
点D到AB边的距离小于点D到AC边的距离
点D到AB边的距离等于点D到AC边的距离
点D到AB边的距离与点D到AC边的距离大小关系不确定
科目:初中数学 来源:黄冈难点课课练八年级数学下册(北师大版) 题型:044
(1)阅读:如图所示△ABC中,∠BAC=![]() ,AB=AC,作∠ABC的平分线交AC于点D,这个点D是线段AC的黄金分割点,且AD>CD.
,AB=AC,作∠ABC的平分线交AC于点D,这个点D是线段AC的黄金分割点,且AD>CD.

(2)在(1)的图形中,还有哪些线段相等,△BCD的三内角各是多少度?
(3)在(1)中,求BC∶AC和BC∶CD的值;
(4)利用(1)的结论,你能作出(1)中线段BD的黄金分割点吗?请作出来,并保留作图痕迹.
科目:初中数学 来源:2012届广东省佛山市南海区九年级上学期期末考试数学试卷(带解析) 题型:解答题
请尝试解决以下问题:
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,
由旋转可得:AB="AD,BG=DE," ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.
(3)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD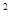 +CE
+CE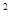 =DE
=DE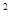 始终成立,请说明理由.
始终成立,请说明理由.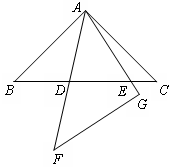
科目:初中数学 来源:2011-2012学年广东省佛山市南海区九年级上学期期末考试数学试卷(解析版) 题型:解答题
请尝试解决以下问题:
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,

由旋转可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.

(2)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD +CE
+CE =DE
=DE 始终成立,请说明理由.
始终成立,请说明理由.

科目:初中数学 来源:不详 题型:解答题

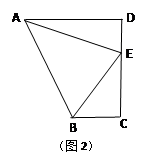
 +CE
+CE =DE
=DE 始终成立,请说明理由.
始终成立,请说明理由.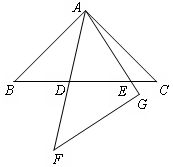
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com