
| 如图所示,直线AB∥CD,E为直线AB上任意一点,F为直线CD上任意一点,通过测量点E到直线CD的距离和点F到直线AB的距离,你发现了什么规律?将你的猜想用自己的语言叙述出来。 |
 |
A.两条平行线间的距离相等 B.两条平行线间的距离不一定相等 |
科目:初中数学 来源: 题型:
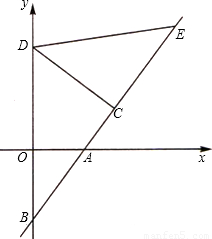
 的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.
的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.科目:初中数学 来源: 题型:
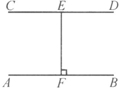 如图所示:直线AB∥CD,且AB、CD之间的距离为6cm,过CD上一点E作AB的垂线段EF,则点E、F之间的距离为
如图所示:直线AB∥CD,且AB、CD之间的距离为6cm,过CD上一点E作AB的垂线段EF,则点E、F之间的距离为科目:初中数学 来源:2009年黑龙江省(鹤、伊、双、绥)升学大考数学试卷(五)(解析版) 题型:解答题
科目:初中数学 来源:不详 题型:解答题
 的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.
的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.科目:初中数学 来源: 题型:解答题
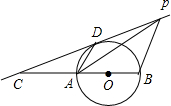
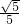 ,O为射线QA上的一动点,⊙O的半径为
,O为射线QA上的一动点,⊙O的半径为 ,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
科目:初中数学 来源:专项题 题型:填空题

科目:初中数学 来源:2011-2012学年江苏省常州市九年级(上)期末数学试卷(解析版) 题型:解答题
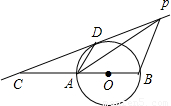
 ,O为射线QA上的一动点,⊙O的半径为
,O为射线QA上的一动点,⊙O的半径为 ,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
,开始时,O点与Q点重合,⊙O沿射线QA方向移动.
科目:初中数学 来源: 题型:填空题
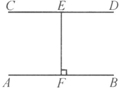 如图所示:直线AB∥CD,且AB、CD之间的距离为6cm,过CD上一点E作AB的垂线段EF,则点E、F之间的距离为________cm,点E到直线AB的距离为________cm.
如图所示:直线AB∥CD,且AB、CD之间的距离为6cm,过CD上一点E作AB的垂线段EF,则点E、F之间的距离为________cm,点E到直线AB的距离为________cm.科目:初中数学 来源:黄石 题型:单选题
| A.15° | B.30° | C.60° | D.90° |
科目:初中数学 来源:2013年山东省枣庄十五中中考数学模拟试卷(解析版) 题型:选择题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com