
如图,将一条线段AB分割成大小两条线段PA、PB,若小段与大段的长度之比等于大段与全段之比,称P为线段AB的黄金分割点.若对一段长20cm的线段进行黄金分割,那么较长线段约为( )cm .(精确到0.1cm , ) ) |
 |
A.12.3cm B.12.4cm C.12.5cm D.12.6cm |
科目:初中数学 来源: 题型:
| 5 |

科目:初中数学 来源:2010-2011学年四川省内江市隆昌三中九年级(上)期中数学试卷(解析版) 题型:填空题
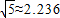 )
)
科目:初中数学 来源:不详 题型:填空题
| 5 |

科目:初中数学 来源: 题型:填空题
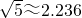 )
)
科目:初中数学 来源:四川省期中题 题型:填空题
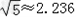 )
)
科目:初中数学 来源: 题型:填空题
科目:初中数学 来源:2013年天津市河西区中考数学一模试卷(解析版) 题型:填空题

科目:初中数学 来源:不详 题型:填空题

科目:初中数学 来源: 题型:
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |
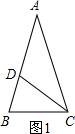
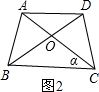
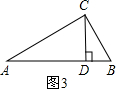
科目:初中数学 来源: 题型:解答题
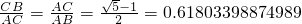 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.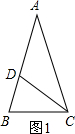


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com