已知函数y=f(x-1)的图像关于点（1，0）对称，且当x∈(-∞，0)时，f(x)+x <0成立（其中 是f(x)的导函数）。若  ， ， ，则a，b，c的大小关系是 |
A．a>b>c B．c>b>a C．c>a>b D．a>c>b |
科目：高中数学 来源：0103 期中题 题型：单选题
<0成立（其中
是f(x)的导函数）。若
，
，
，则a，b，c的大小关系是科目：高中数学 来源： 题型：013
已知函数y=f（x），则它的反函数的图像关于原点对称的函数是（ ）
A．y=-f（x） B．y=f -1（x）
C．y=-f -1（x） D．y=-f -1 （-x）
科目：高中数学 来源：数学教研室 题型：013
A．y=-f（x） B．y=f -1（x）
C．y=-f -1（x） D．y=-f -1 （-x）
科目：高中数学 来源： 题型：
已知函数f(x)= 
+lnx的图像在点P(m,f(m))处的切线方程为y=x ,
设
．
（1）求证：当
恒成立；
（2）试讨论关于
的方程：
根的个数．
科目：高中数学 来源：不详 题型：解答题
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
． 
恒成立；
的方程：
根的个数．科目：高中数学 来源： 题型：044
已知函数f(x)=x2-1(x³1)的图像是C1，曲线C2与C1关于直线y=x对称．
（1）求曲线C2的方程y=g(x)；
（2）设函数y=g(x)的定义或为M，x1，x2ÎM，且x1¹x2．求证|g(x1)-g(x2)|<|x1-x2|；
（3）设A，B是曲线C2上任意不同的两点，证明直线AB与直线y=x必相交．
科目：高中数学 来源：数学教研室 题型：044
（1）求曲线C2的方程y=g(x)；
（2）设函数y=g(x)的定义或为M，x1，x2ÎM，且x1¹x2．求证|g(x1)-g(x2)|<|x1-x2|；
（3）设A，B是曲线C2上任意不同的两点，证明直线AB与直线y=x必相交．
科目：高中数学 来源：2012届山东省高二下学期期末考试理科数学 题型：选择题
已知函数y=f（x）是定义在R上的增函数，函数y=f(x-1)的图像关于点（1，0）对称，若对任的x,y∈R，不等式f(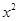
-6x+21)+f(
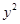-8y)<0恒成立，则当x>3时，
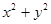的取值范围是（ ）
A (3,7) B (9,25) C (13,49) D (9,49)
科目：高中数学 来源： 题型：单选题
已知函数y=f（x）是定义在R上的增函数，函数y=f(x-1)的图像关于点（1，0）对称，若对任的x,y∈R，不等式f(
-6x+21)+f(
-8y)<0恒成立，则当x>3时，
的取值范围是（ ）
A (3,7) B (9,25) C (13,49) D (9,49)
科目：高中数学 来源：不详 题型：单选题
-6x+21)+f(
-8y)<0恒成立，则当x>3时，
的取值范围是（ ） 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com