| 平面直角坐标系中，若过点P(-2，t)、Q(t，4) 的直线斜率为1，则t= |
A.1
B.2
C.3
D.1或2 |
相关习题
科目：高中数学
来源：0111 期中题
题型：单选题
平面直角坐标系中，若过点P(-2，t)、Q(t，4) 的直线斜率为1，则t=
查看答案和解析>>
科目：高中数学
来源：
题型：
平面直角坐标系中，若过点P（-2，t）、Q（t，4） 的直线斜率为1，则t=（ ）
查看答案和解析>>
科目：高中数学
来源：不详
题型：单选题
平面直角坐标系中，若过点P（-2，t）、Q（t，4） 的直线斜率为1，则t=（ ）
查看答案和解析>>
科目：高中数学
来源：2008-2009学年浙江省温州中学高一（下）期中数学试卷（解析版）
题型：选择题
平面直角坐标系中，若过点P（-2，t）、Q（t，4） 的直线斜率为1，则t=（ ）
A．1
B．2
C．3
D．1或2
查看答案和解析>>
科目：高中数学
来源：
题型：单选题
平面直角坐标系中，若过点P（-2，t）、Q（t，4） 的直线斜率为1，则t=
- A.
1
- B.
2
- C.
3
- D.
1或2
查看答案和解析>>
科目：高中数学
来源：
题型：
平面直角坐标系中，已知直线l：x=4，定点F（1，0），动点P（x，y）到直线l的距离是到定点F的距离的2倍．
（1）求动点P的轨迹C的方程；
（2）若M为轨迹C上的点，以M为圆心，MF长为半径作圆M，若过点E（-1，0）可作圆M的两条切线EA，EB（A，B为切点），求四边形EAMB面积的最大值．
查看答案和解析>>
科目：高中数学
来源：
题型：
平面直角坐标系中，O为坐标原点，已知两定点A（1，0），B（0，－1），动点P（x，y）满足：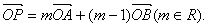
（1）求点P的轨迹方程；
（2）设点P的轨迹与双曲线
交于相异两点M、N，若以MN为直径的圆经过原点，且双曲线C的离心率等于
，求双曲线C的方程.
查看答案和解析>>
科目：高中数学
来源：2011年广东省深圳市高考数学二模试卷（理科）（解析版）
题型：解答题
平面直角坐标系中，已知直线l：x=4，定点F（1，0），动点P（x，y）到直线l的距离是到定点F的距离的2倍．
（1）求动点P的轨迹C的方程；
（2）若M为轨迹C上的点，以M为圆心，MF长为半径作圆M，若过点E（-1，0）可作圆M的两条切线EA，EB（A，B为切点），求四边形EAMB面积的最大值．
查看答案和解析>>
科目：高中数学
来源：2011年江苏省南京外国语学校高三考前适应性测试数学试卷（解析版）
题型：解答题
平面直角坐标系中，已知直线l：x=4，定点F（1，0），动点P（x，y）到直线l的距离是到定点F的距离的2倍．
（1）求动点P的轨迹C的方程；
（2）若M为轨迹C上的点，以M为圆心，MF长为半径作圆M，若过点E（-1，0）可作圆M的两条切线EA，EB（A，B为切点），求四边形EAMB面积的最大值．
查看答案和解析>>
科目：高中数学
来源：
题型：
在平面直角坐标系中，O为坐标原点，已知两点M （1，-3）、N（5，1），若点C满足
=t
+（1-t）
（t∈R），点C的轨迹与抛物线：y
2=4x交于A、B两点．
（1）求证：
⊥
；
（2）在x轴上是否存在一点P （m，0），使得过点P任作抛物线的一条弦，并以该弦为直径的圆都过原点．若存在，请求出m的值及圆心的轨迹方程；若不存在，请说明理由．
查看答案和解析>>
