
科目:高中数学 来源: 题型:
| 8 |
| 3 |
| OM |
| ON |
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、0 |
科目:高中数学 来源:2008-2009学年浙江省温州中学高一(下)期中数学试卷(解析版) 题型:选择题
 相交于两点M,N.若b2=2(k2+1),则
相交于两点M,N.若b2=2(k2+1),则
 =( )
=( )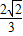


科目:高中数学 来源: 题型:
| 1 | 3 |
科目:高中数学 来源: 题型:
| x2 |
| 2 |
| OA |
| OB |
| 2 |
| 3 |
| OA |
| OB |
| 2 |
| 3 |
| 3 |
| 4 |
科目:高中数学 来源:不详 题型:解答题
| x2 |
| 2 |
| OA |
| OB |
| 2 |
| 3 |
| OA |
| OB |
| 2 |
| 3 |
| 3 |
| 4 |
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
科目:高中数学 来源:2010-2011学年浙江省台州中学高三(上)第二次统练数学试卷(理科)(解析版) 题型:解答题
 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.科目:高中数学 来源:2010-2011学年浙江省台州中学(上)第二次统练数学试卷(理科)(解析版) 题型:解答题
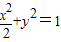 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.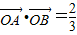 ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.科目:高中数学 来源:2008年上海市普陀区高考数学二模试卷(解析版) 题型:解答题
 .
.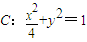 上;
上; ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;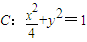 内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com