练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设f(x)是定义在R上的奇函数，且当x＞0时，f(x)=2x-3，则f(-2)等于

    A．1
    B．
    C．-1
    D．
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    设f(x)是定义在R上的奇函数，且f(1+x)=f(1-x),下列说法①f(x+2)=f(x);②f(x+4)=-f(x);③f(1)+f(2)+f(3)+f(4)=0;④f(x+4)=f(x).正确的是（    ）

    A.①②③                B.①③                   C.③④               D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有恒成立，则不等式的解集是

    (A) (-2,0) ∪(2,+∞)    (B) (-2,0) ∪(0,2)   (C) (-∞,-2)∪(2,+∞)    (D) (-∞,-2)∪(0,2)

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河北保定安新县第一中学高三4月模拟考试数学试卷（解析版） 题型：选择题

    设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有恒成立，则不等式的解集是

    A．(-2,0) ∪(2,+∞)                        B．(-2,0) ∪(0,2)

    C．(-∞,-2)∪(2,+∞)                        D．(-∞,-2)∪(0,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河南省镇平一高高三下学期第三次周考理科数学试卷 题型：填空题

    设f(x)是定义在R上的奇函数，且当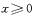时，，若对任意的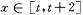，不等式恒成立，则实数t的取值范围是. _______

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三上学期期末考试文科数学 题型：选择题

    设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有恒成立，则不等式 的解集是

    A.(-2,0) ∪(2,+∞)   B.(-2,0) ∪(0,2)  C.(-∞,-2)∪(2,+∞)    D.(-∞,-2)∪(0,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省高三10月月考文科数学试卷 题型：选择题

    设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有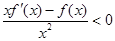恒成立，

     

    则不等式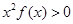的解集是

    A. (-2,0) ∪(2,+∞)     B. (-2,0) ∪(0,2)    C. (-∞,-2)∪(2,+∞)     D. (-∞,-2)∪(0,2)

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学函数的图象奇偶性、周期性专项训练（河北） 题型：解答题

    设f(x)是定义在R上的奇函数，且对任意实数x恒满足f(x＋2)＝－f(x)，当x∈[0,2]时，f(x)＝2x－x2.

    (1)求证：f(x)是周期函数．

    (2)当x∈[2,4]时，求f(x)的解析式．

    (3)计算f(0)＋f(1)＋f(2)＋…＋f(2011)

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设f(x)是定义在R上的奇函数，且f(2)=0,当x>0时，有恒成立，则不等式的解集是

    A．(-2,0) ∪(2,+∞)B．(-2,0) ∪(0,2)
    C．(-∞,-2)∪(2,+∞)D．(-∞,-2)∪(0,2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设f(x)是定义在R上的奇函数，且对任意实数x，恒有f(x＋2)＝－f(x)，当x∈[0，2]时，f(x)＝2x－x2.
    (1)求证：f(x)是周期函数；
    (2)当x∈[2，4]时，求f(x)的解析式；
    (3)计算f(0)＋f(1)＋f(2)＋…＋f(2014)的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设f(x)是定义在R上的奇函数，且对任意实数x恒满足f(x＋2)＝－f(x)，当x∈[0,2]时，f(x)＝2x－x2.
    (1)求证：f(x)是周期函数．
    (2)当x∈[2,4]时，求f(x)的解析式．
    (3)计算f(0)＋f(1)＋f(2)＋…＋f(2011)

    查看答案和解析>>


    同步练习册答案