已知数列｛an｝满足：a1= ，且an= （n≥2，n∈N*）。对于一切正整数n，不等式a1·a2·……an和2·n！的关系判断正确的是 |
A.a1·a2·……an＞2·n！， B.a1·a2·……an=2·n！， C.a1·a2·……an<2·n！， D.a1·a2·……an≤2·n！， |
科目：高中数学 来源：0116 期中题 题型：解答题
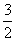，且an=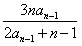
（n≥2，n∈N*）。科目：高中数学 来源：2011-2012学年重庆市高三上学期第三次理科数学测试卷（解析版） 题型：解答题
已知数列｛an｝满足：a1＝
，且an＝
（1） 求数列｛an｝的通项公式；
（2） 证明：对于一切正整数n，不等式a1·a2·……an<2·n！
科目：高中数学 来源：不详 题型：解答题
，且an＝
科目：高中数学 来源： 题型：
（06年江西卷理）（14分）
已知数列｛an｝满足：a1＝
，且an＝
（1）求数列｛an｝的通项公式；
（2）证明：对于一切正整数n，不等式a1?a2?……an<2?n！
科目：高中数学 来源： 题型：
已知｛an｝是正数组成的数列，a1=1，且点（
）（n
N*）在函数y=x2+1的图象上．
（Ⅰ）求数列｛an｝的通项公式；
（Ⅱ）若数列｛bn｝满足b1=1，bn+1=bn+
，求证：bn?bn+2＜b2n+1．
科目：高中数学 来源： 题型：
）（n
N*）在函数y=x2+1的图象上.(Ⅰ)求数列｛an｝的通项公式；
(Ⅱ)若列数｛bn｝满足b1=1,bn+1=bn+
，求证：bn ·bn+2＜
。
科目：高中数学 来源： 题型：
（福建卷文20）已知｛an｝是正数组成的数列，a1=1，且点（
）（n
N*）在函数y=x2+1的图象上.
(Ⅰ)求数列｛an｝的通项公式；
(Ⅱ)若列数｛bn｝满足b1=1,bn+1=bn+
，求证：bn ·bn+2＜b2n+1.
科目：高中数学 来源： 题型：
（福建卷文20）已知｛an｝是正数组成的数列，a1=1，且点（
）（n
N*）在函数y=x2+1的图象上.
(Ⅰ)求数列｛an｝的通项公式；
(Ⅱ)若列数｛bn｝满足b1=1,bn+1=bn+
，求证：bn ·bn+2＜b2n+1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，且an＝
，且an＝