| 经过圆(x-1)2+y2=1的圆心M,且与直线x-y=0垂直的直线方程是 |
A.x-y+1=0
B.x-y-1=0
C.x+y-1=0
D.x+y+1=0 |
相关习题
科目:高中数学
来源:广东省模拟题
题型:单选题
经过圆(x-1)2+y2=1的圆心M,且与直线x-y=0垂直的直线方程是
A.x-y+1=0
B.x-y-1=0
C.x+y-1=0
D.x+y+1=0
查看答案和解析>>
科目:高中数学
来源:
题型:
(理)已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一个动圆与这两个圆都外切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)若经过点M2的直线与(Ⅰ)中的轨迹C有两个交点A、B,求|AM1|•|BM1|的最小值.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
(理)已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一个动圆与这两个圆都外切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)若经过点M2的直线与(Ⅰ)中的轨迹C有两个交点A、B,求|AM1|•|BM1|的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(理)已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一个动圆与这两个圆都外切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)若经过点M2的直线与(Ⅰ)中的轨迹C有两个交点A、B,求|AM1|•|BM1|的最小值.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年北京师大附中高三(上)第四次月考数学试卷(文科)(解析版)
题型:解答题
已知两圆Q1:(x+1)
2+y
2=

和Q2:(x-1)
2+y
2=
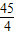
,动圆P与⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线l与点P的轨迹交于不同两点A、B,试推断是否存在直线l,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:2010年广东省珠海市高考数学二模试卷(文科)(解析版)
题型:解答题
已知两圆Q1:(x+1)
2+y
2=

和Q2:(x-1)
2+y
2=
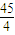
,动圆P与⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线l与点P的轨迹交于不同两点A、B,试推断是否存在直线l,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:2010年湖南省高考数学考前冲刺试卷(解析版)
题型:解答题
已知两圆Q1:(x+1)
2+y
2=

和Q2:(x-1)
2+y
2=

,动圆P与⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线l与点P的轨迹交于不同两点A、B,试推断是否存在直线l,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省珠海市高三(下)质量监测数学试卷(文科)(解析版)
题型:解答题
已知两圆Q1:(x+1)
2+y
2=

和Q2:(x-1)
2+y
2=

,动圆P与⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线l与点P的轨迹交于不同两点A、B,试推断是否存在直线l,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知圆M经过点(1,2),且圆心为(2,0),那么圆M的方程为( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年贵州省毕节地区黔西二中高二(上)期中数学试卷(解析版)
题型:选择题
已知圆M经过点(1,2),且圆心为(2,0),那么圆M的方程为( )
A.(x-2)2+y2=5
B.(x+2)2+y2=5
C.(x-2)2+y2=3
D.(x+2)2+y2=3
查看答案和解析>>

 和Q2:(x-1)2+y2=
和Q2:(x-1)2+y2=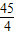 ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切. 和Q2:(x-1)2+y2=
和Q2:(x-1)2+y2=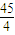 ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切. 和Q2:(x-1)2+y2=
和Q2:(x-1)2+y2= ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切. 和Q2:(x-1)2+y2=
和Q2:(x-1)2+y2= ,动圆P与⊙O1外切,且与⊙O2内切.
,动圆P与⊙O1外切,且与⊙O2内切.