
科目:高中数学 来源: 题型:013
已知AB是异面直线l1、l2的公垂线段,且AB=3,异面直线l1、l2成30°角,在直线l1上取AP=6,则点P到直线l2的距离等于( )
A.6 B.![]()
C.6或![]() D.
D.![]()
科目:高中数学 来源:数学教研室 题型:013
A.6 B.![]()
C.6或![]() D.
D.![]()
科目:高中数学 来源:2009-2010学年北京市丰台区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 时,圆P恰与两直线l1、l2相切,试求圆P的方程;
时,圆P恰与两直线l1、l2相切,试求圆P的方程; 时,求四边形ABDC的面积;
时,求四边形ABDC的面积; )时,求证四边形ABDC的对角线交点位置与k的取值无关.
)时,求证四边形ABDC的对角线交点位置与k的取值无关.科目:高中数学 来源: 题型:
| 3 |
| PA |
| PB |
科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
科目:高中数学 来源:2011-2012学年福建师大附中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,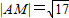 ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
| 1 | 2 |
科目:高中数学 来源: 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com