
科目:高中数学 来源:广东省恩城中学2009届高三上学期模拟考试(数学文) 题型:013
若a,b是常数,则“a>0且b2-4a<0”是“对任意x∈R,有ax2+bx+1>0”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
科目:高中数学 来源:山东省青岛二中2012届高三下学期期中考试数学文科试题 题型:022
①命题“若a<b,则am2<bm2”的否命题是假命题.
②设α,β为两个不同的平面,直线l![]() α,则l⊥β是α⊥β成立的充分不必要条件.
α,则l⊥β是α⊥β成立的充分不必要条件.
③命题“![]() x∈R,x2-x>0”的否定是“
x∈R,x2-x>0”的否定是“![]() x∈R,x2-x<0”.
x∈R,x2-x<0”.
④已知x∈R,则“x>1”是“x>2”的充分不必要条件.
上面说法正确的是________.
科目:高中数学 来源:2011-2012年山西省忻州一中高三(上)期中数学试卷(文科)(解析版) 题型:填空题
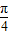 )时,函数y=sinx+
)时,函数y=sinx+ 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.科目:高中数学 来源:2011-2012学年山西省忻州一中高三(上)期中数学试卷(理科)(解析版) 题型:填空题
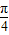 )时,函数y=sinx+
)时,函数y=sinx+ 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.科目:高中数学 来源: 题型:填空题
 )时,函数y=sinx+
)时,函数y=sinx+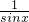 的最小值为2;
的最小值为2; 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.科目:高中数学 来源:2002年高中会考数学必备一本全2002年1月第1版 题型:013
若x∈R,则(1-|x|)(1+x)>0的充要条件是
[ ]
科目:高中数学 来源:山西省忻州一中2012届高三上学期期中考试数学文科试题 题型:022
下列四个命题中
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;
②当x∈(0,![]() )时,函数y=sinx+
)时,函数y=sinx+![]() 的最小值为2;
的最小值为2;
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x-![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是________
科目:高中数学 来源:山西省忻州一中2012届高三上学期期中考试数学理科试题 题型:022
下列四个命题中
①若a,b,cÎ R,则“ac2>bc2”是“a>b”成立的充分不必要条件;
②当xÎ
(0,![]() )时,函数y=sinx+
)时,函数y=sinx+![]() 的最小值为2;
的最小值为2;
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
④函数f(x)=lnx+x-![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
其中正确命题的序号是________
科目:高中数学 来源: 题型:
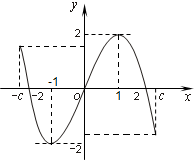 如图所示,f(x)是定义在区间[-c,c](c>0)上的奇函数,令g(x)=af(x)+b,并有关于函数g(x)的四个论断:
如图所示,f(x)是定义在区间[-c,c](c>0)上的奇函数,令g(x)=af(x)+b,并有关于函数g(x)的四个论断:| g(n)-g(m) | n-m |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com