设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),设集合
 ,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为 ,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为 |
A.20
B.18
C.16
D.14 |
相关习题
科目:高中数学
来源:专项题
题型:单选题
设函数f(x)=(x
2-10x+c
1)(x
2-10x+c
2)(x
2-10x+c
3)(x
2-10x+c
4)(x
2-10x+c
5),设集合M={x|f(x)=0}={x
1,x
2,…,x
9}

N*,设c
1≥c
2≥c
3≥c
4≥c
5,则c
1-c
5为
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:0103 期中题
题型:单选题
设函数f(x)=(x
2-10x+c
1)( x
2-10x+c
2)( x
2-10x+c
3)( x
2-10x+c
4)( x
2-10x+c
5),设集合M={x|f(x)=0}={x
1,x
2,x
3,…,x
9}
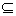
N*,设c
1≥c
2≥c
3≥c
4≥c
5,则c
1-c
5为
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:上海模拟题
题型:单选题
设函数f(x)=(x
2-10x+c
1)(x
2-10x+c
2)(x
2-10x+c
3)(x
2-10x+c
4)(x
2-10x+c
5),设集合
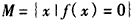
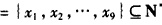
,设c
1≥c
2≥c
3≥c
4≥c
5 ,则c
1-c
5为
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:
题型:
10、设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
查看答案和解析>>
科目:高中数学
来源:2011-2012学年浙江省杭州市萧山中学高三(上)摸底数学试卷(文科)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:2009-2010学年上海市十三校高三(上)第一次联考数学试卷(文科)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:2009-2010学年上海市十三校高三(上)第一次联考数学试卷(理科)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷02(文科)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷07(文科)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>
科目:高中数学
来源:2010年湖北省荆州市高三质量检测数学试卷(2)(解析版)
题型:选择题
设函数f(x)=(x2-10x+c1)(x2-10x+c2)(x2-10x+c3)(x2-10x+c4)(x2-10x+c5),集合M={x|f(x)=0}={x1,x2,…,x9}⊆N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为( )
A.20
B.18
C.16
D.14
查看答案和解析>>


 ,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为
,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为 N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为
N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为 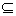 N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为
N*,设c1≥c2≥c3≥c4≥c5,则c1-c5为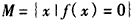
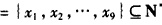 ,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为
,设c1≥c2≥c3≥c4≥c5 ,则c1-c5为