
| 在数列{an}中,a1=1,若对所有的n≥2,都有a1a2…an=n2,则a3+a5等于 |
A、  B、  C、  D、  |
科目:高中数学 来源: 题型:
| an+2 |
| an+1 |
| an+1 |
| an |
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
| n•3n |
| 3n-1 |
科目:高中数学 来源: 题型:
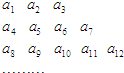 将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:
将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:| 2 |
| 5 |
| 1 |
| k |
| 1-x2 |
| x |
| 1 |
| 1000 |
| 1 |
| 100 |
科目:高中数学 来源: 题型:
|
| 2 |
| 5 |
| 1 |
| k |
| 1-x2 |
| x |
| 1 |
| 200 |
| 1 |
| 20 |
科目:高中数学 来源: 题型:解答题
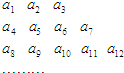 将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:
将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知: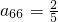 .请解答以下问题:
.请解答以下问题: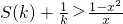 在
在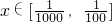 上有解,求正整数k的取值范围.
上有解,求正整数k的取值范围.科目:高中数学 来源:成都一模 题型:解答题
| 2n |
| 2n |
科目:高中数学 来源:不详 题型:解答题
|
| 2 |
| 5 |
| 1 |
| k |
| 1-x2 |
| x |
| 1 |
| 200 |
| 1 |
| 20 |
科目:高中数学 来源:2013年四川省成都市高考数学一模试卷(文科)(解析版) 题型:解答题
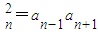 ,n∈N*.
,n∈N*. 成立?若存在,求出所有符合条件的(m,n);若不存在,请说明理由.
成立?若存在,求出所有符合条件的(m,n);若不存在,请说明理由.科目:高中数学 来源:2010-2011学年上海市十三校高三(下)第二次联考数学试卷(文科)(解析版) 题型:解答题
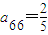 .请解答以下问题:
.请解答以下问题: 在
在 上有解,求正整数k的取值范围.
上有解,求正整数k的取值范围.
科目:高中数学 来源:2010-2011学年上海市十三校高三(下)第二次联考数学试卷(理科)(解析版) 题型:解答题
 .请解答以下问题:
.请解答以下问题: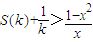 在
在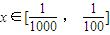 上有解,求正整数k的取值范围.
上有解,求正整数k的取值范围.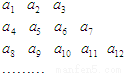
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com