科目：高中数学 来源：同步题 题型：单选题

查看答案和解析>>

科目：高中数学 来源： 题型：

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

查看答案和解析>>

科目：高中数学 来源：2012-2013学年广东省揭阳一中、潮州金山中学高三（上）联合摸底数学试卷（文科）（解析版） 题型：解答题

在数列{a_n}中，已知a₁=1，a_n=a_n-1+a_n-2+…+a₂+a₁（n∈N*，n≥2）．
（1）求数列{a_n}的通项公式；
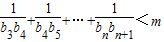（2）若b_n=log₂a_n，对于任意的n∈N*，且n≥3恒成立，求m的取值范围．

查看答案和解析>>

科目：高中数学 来源：2009-2010学年四川省南充一中高三（下）6月适应性考试数学试卷（文科）（解析版） 题型：解答题

在数列{a_n}中，已知a₁=1，a_n=a_n-1+a_n-2+…+a₂+a₁（n∈N*，n≥2）．
（1）求数列{a_n}的通项公式；
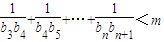（2）若b_n=log₂a_n，对于任意的n∈N*，且n≥3恒成立，求m的取值范围．

查看答案和解析>>

科目：高中数学 来源：2012年湖南省高考数学压轴卷（文科）（解析版） 题型：解答题

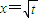已知在数列{a_n}中，a₁=t，a₂=t²（t＞0且t≠1）．是函数f（x）=a_n-1x³-3[（t+1）a_n-a_n+1]x+1（n≥2）的一个极值点．
（1）证明数列{a_n+1-a_n}是等比数列，并求数列{a_n}的通项公式；
（2）记，当t=2时，数列{b_n}的前n项和为S_n，求使S_n＞2008的n的最小值；
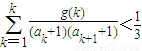（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源：2010年山东省东营市高三一轮复习数学试卷（理科）（解析版） 题型：解答题

已知在数列{a_n}中，a₁=t，a₂=t²（t＞0且t≠1）．是函数f（x）=a_n-1x³-3[（t+1）a_n-a_n+1]x+1（n≥2）的一个极值点．
（1）证明数列{a_n+1-a_n}是等比数列，并求数列{a_n}的通项公式；
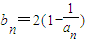（2）记，当t=2时，数列{b_n}的前n项和为S_n，求使S_n＞2008的n的最小值；
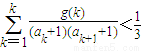（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源：高考数学最后冲刺必读题解析30讲（30）（解析版） 题型：解答题

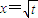已知在数列{a_n}中，a₁=t，a₂=t²（t＞0且t≠1）．是函数f（x）=a_n-1x³-3[（t+1）a_n-a_n+1]x+1（n≥2）的一个极值点．
（1）证明数列{a_n+1-a_n}是等比数列，并求数列{a_n}的通项公式；
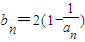（2）记，当t=2时，数列{b_n}的前n项和为S_n，求使S_n＞2008的n的最小值；
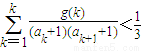（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

查看答案和解析>>

科目：高中数学 来源：2007-2008学年重庆八中高三（下）第一次月考数学试卷（理科）（解析版） 题型：选择题

已知正整数数列{a_n}中，a₁=3，且对于任意大于1的整数n，点总在直线上，则=（ ）
A．0
B．1
C．2
D．3

查看答案和解析>>