
科目:高中数学 来源:成都一模 题型:解答题
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2xn | ||
1+
|
| 1 |
| f(xn) |
| m-4 |
| 3 |
科目:高中数学 来源:2006年四川省成都市高考数学一模试卷(理科)(解析版) 题型:解答题
 ,且对x,y∈(-1,1)时,有
,且对x,y∈(-1,1)时,有 .
. ,求数列{f(xn)}的通项公式;
,求数列{f(xn)}的通项公式; 的前n项和,问是否存在正整数m,使得对任意的n∈N*,有
的前n项和,问是否存在正整数m,使得对任意的n∈N*,有 成立?若存在,求出m的最小值;若不存在,则说明理由.
成立?若存在,求出m的最小值;若不存在,则说明理由.科目:高中数学 来源:2007年福建省厦门市普通中学高中毕业班质量检查数学(文科)试题 题型:044
已知定义在(-1,1)上的函数f(x)满足f![]() =1,且对x、y∈(-1,1)时,有f(x)-f(y)=
=1,且对x、y∈(-1,1)时,有f(x)-f(y)=![]() .
.
(1)判断f(x)在(-1,1)上的奇偶性,并证明之;
(2)令x1=![]() ,xn+1=
,xn+1=![]() ,求数列{f(xn)}的通项公式;
,求数列{f(xn)}的通项公式;
(3)设Tn为数列{![]() }的前n项和,问是否存在正整数m,使得对任意的n∈N*,有Tn<
}的前n项和,问是否存在正整数m,使得对任意的n∈N*,有Tn<![]() 成立?若存在,求出m的最小值;若不存在,则说明理由.
成立?若存在,求出m的最小值;若不存在,则说明理由.
科目:高中数学 来源:茂名市一中2007届高三第二次调研考试试卷、数学卷(文科) 题型:044
已知定义在(-1,1)上的函数f(x)满足![]() ,且对x,y∈(-1,1)时,有
,且对x,y∈(-1,1)时,有![]() (Ⅰ)判断f(x)在(-1,1)上的奇偶性,并加以证明;
(Ⅰ)判断f(x)在(-1,1)上的奇偶性,并加以证明;
(Ⅱ)令![]() ,求数列{f(x)}的通项公式;
,求数列{f(x)}的通项公式;
(Ⅲ)设Tn为数列{![]() }的前n项和,问是否存在正整数m,使得对任意的n∈N*,有
}的前n项和,问是否存在正整数m,使得对任意的n∈N*,有![]() 成立?若存在,求出m的最小值,若不存在,则说明理由.
成立?若存在,求出m的最小值,若不存在,则说明理由.
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| a+b |
| 2 |
| ab |
科目:高中数学 来源: 题型:
|
科目:高中数学 来源:松江区模拟 题型:解答题
| 1 |
| 2 |
| a+b |
| 2 |
| ab |
科目:高中数学 来源:2006年上海市八校高三联考数学试卷(松江二中、青浦、七宝、育才、市二、行知、位育)(解析版) 题型:解答题
 x3,x∈(-2,2)为正常数.
x3,x∈(-2,2)为正常数.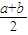
 (当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(当且仅当a=b时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com