在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量a=(a,b),从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为n,其中面积不超过2的平行四边形的个数为m,则 |
A.
B.
C.
D. |
相关习题
科目:高中数学
来源:
题型:
在集合1,2,3,4,5中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作为平行四边形的个数为n,其中面积不超过4的平行四边形的个数m,则
=( )
查看答案和解析>>
科目:高中数学
来源:
题型:
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则
=( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在集合1,2,3,4,5中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作为平行四边形的个数为n,其中面积不超过4的平行四边形的个数m,则
=( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则
=( )
查看答案和解析>>
科目:高中数学
来源:2011年四川省高考数学试卷(文科)(解析版)
题型:选择题
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量

=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则

=( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2011年四川省高考数学试卷(理科)(解析版)
题型:选择题
在集合1,2,3,4,5中任取一个偶数a和一个奇数b构成以原点为起点的向量

=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作为平行四边形的个数为n,其中面积不超过4的平行四边形的个数m,则

=( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:
题型:单选题
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量 =(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则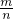 =
=
- A.
- B.
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:四川省高考真题
题型:单选题
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
a=(a,b),从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为n,其中面积等于2的平行四边形的个数为m,则

查看答案和解析>>
科目:高中数学
来源:四川省高考真题
题型:单选题
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
a=(a,b),从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则
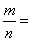
查看答案和解析>>
科目:高中数学
来源:2011年普通高等学校招生全国统一考试数学理科试题四川卷
题型:013
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则
[ ]
A.
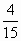
B.

C.

D.
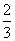
查看答案和解析>>






 =(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则 =( )
=( )



 =(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作为平行四边形的个数为n,其中面积不超过4的平行四边形的个数m,则
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作为平行四边形的个数为n,其中面积不超过4的平行四边形的个数m,则 =( )
=( )



 =(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则
=(a,b)从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形,记所有作成平行四边形的个数为n,其中面积等于4的平行四边形的个数为m,则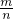 =
=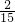

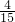


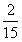

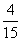
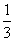
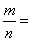

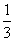
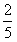
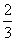
![]()
![]()
![]()
![]()
![]()