练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知双曲线C：(a＞0，b＞0)的右焦点为F，过F且斜率为的直线交C于A、B两点．若，则C的离心率为

    A、
    B、
    C、
    D、
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：高考真题 题型：单选题

    已知双曲线C：(a＞0，b＞0)的右焦点为F，过F且斜率为的直线交C于A、B两点．若，则C的离心率为
    [     ]
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：高中数学 来源：吉林省吉林一中2009－2010学年高二上学期期末考试数学试题 题型：044

    已知双曲线C：(a＞0，b＞0)的离心率e＝2，A，B为双曲线上两点，线段AB的垂直平分线为x－y－2＝0，且|AB|＝．

    ①求双曲线C经过二、四象限的渐近线的倾斜角

    ②试判断在椭圆C的长轴上是否存在一定点N(a，0)，使椭圆上的动点M满足的最小值为3，若存在求出所有可能的a值，若不存在说明理由．

    查看答案和解析>>

    科目：高中数学 来源：山东省聊城市水城中学2011－2012学年高二下学期阶段测试(二)数学理科试题 题型：044

    已知双曲线C：(a＞0，b＞0)的右焦点为F2，F2在C的两条渐近线上的射影分别为P、Q，O是坐标原点，且四边形OPF2Q是边长为2的正方形．

    (Ⅰ)求双曲线C的方程；

    (Ⅱ)过F2的直线交C于A、B两点，线段AB的中点为M，问|MA|＝|MB|＝|MO|是否能成立？若成立，求直线的方程；若不成立，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：福州一中高三数学模拟试卷(一)(文科) 题型：044

    已知双曲线C：(a＞0，b＞0)的离心率e＝2，A(0，－b)、B(a，0)，坐标原点O到直线AB的距离为．

    (1)求双曲线C的方程；

    (2)设F为双曲线C的右焦点，直线l过点F且与双曲线C的右支交于不同的两点P、Q，若＝10，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：山东省聊城市东阿一中2011－2012学年高二下学期阶段性测试(二)数学理科试题 题型：044

    已知双曲线C：(a＞0，b＞0)的右焦点为F2，F2在C的两条渐近线上的射影分别为P、Q，O是坐标原点，且四边形OPF2Q是边长为2的正方形．

    (Ⅰ)求双曲线C的方程；

    (Ⅱ)过F2的直线交C于A、B两点，线段AB的中点为M，问|MA|＝|MB|＝|MO|是否能成立？若成立，求直线的方程；若不成立，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：天津模拟题 题型：单选题

    已知双曲线C：(a＞0，b＞0)半焦距为c，过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点，若抛物线y2=4cx的准线被双曲线C截得的弦长为be2(e为双曲线C的离心率)，则e的值为
    [     ]
    A.或
    B.
    C.3或
    D.

    查看答案和解析>>

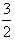
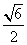
    科目：高中数学 来源：2007年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型：013

    已知双曲线C：(a＞0，b＞0)，以C的右焦点为圆心且与C的浙近线相切的圆的半径是

    [　　]

    A．

    B．

    C．a

    D．b

    查看答案和解析>>

    科目：高中数学 来源：北京高考真题 题型：解答题

    已知双曲线C：(a＞0，6 ＞0)的离心率为，右准线方程为x=，
    (Ⅰ)求双曲线C的方程；
    (Ⅱ)已知直线x-y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线＝1(a＞0，b＞0)的两条渐近线均和圆C：x2＋y2－6x＋5＝0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为(　　)

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西省吉安市白鹭洲中学高三（上）期中数学试卷（文科）（解析版） 题型：选择题

    已知双曲线-=1（a＞0，b＞0）的两条渐近线均和圆C：x2+y2-6x+5=0相切，则该双曲线离心率等于（ ）
    A．
    B．
    C．
    D．

    查看答案和解析>>


    同步练习册答案