练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知数列{an}是等差数列，如果a1+a3=12，那么a2=

    A．4
    B．6
    C．8
    D．10
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知数列{an}是等差数列，如果a1+a3＝12，那么a2＝


    1. A.
      4
    2. B.
      6
    3. C.
      8
    4. D.
      10

    查看答案和解析>>

    科目：高中数学 来源：云南省模拟题 题型：单选题

    已知数列{an}是等差数列，如果a1+a3=12，那么a2=
    [     ]
    A．4
    B．6
    C．8
    D．10

    查看答案和解析>>

    科目：高中数学 来源：云南省绿春第一中学2011届高三第二次复习统一检测理科数学试题 题型：013

    已知数列{an}是等差数列，如果a1＋a3＝12，那么a2＝

    [　　]
    A．

    4

    B．

    6

    C．

    8

    D．

    10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}是等差数列，cn=an2-an+12（n∈N*）
    （1）判断数列{cn}是否是等差数列，并说明理由；
    （2）如果a1+a3+…+a25=130，a2+a4+…+a26=143-13k（k为常数），试写出数列{cn}的通项公式；
    （3）在（2）的条件下，若数列{cn}得前n项和为Sn，问是否存在这样的实数k，使Sn当且仅当n=12时取得最大值．若存在，求出k的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知数列{an}是等差数列，cn=an2-an+12（n∈N*）
    （1）判断数列{cn}是否是等差数列，并说明理由；
    （2）如果a1+a3+…+a25=130，a2+a4+…+a26=143-13k（k为常数），试写出数列{cn}的通项公式；
    （3）在（2）的条件下，若数列{cn}得前n项和为Sn，问是否存在这样的实数k，使Sn当且仅当n=12时取得最大值．若存在，求出k的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省泰州市泰兴市重点中学高三第一次检测数学试卷（文科）（解析版） 题型：解答题

    已知数列{an}是等差数列，cn=an2-an+12（n∈N*）
    （1）判断数列{cn}是否是等差数列，并说明理由；
    （2）如果a1+a3+…+a25=130，a2+a4+…+a26=143-13k（k为常数），试写出数列{cn}的通项公式；
    （3）在（2）的条件下，若数列{cn}得前n项和为Sn，问是否存在这样的实数k，使Sn当且仅当n=12时取得最大值．若存在，求出k的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：江苏泰兴重点中学2011届高三第一次检测数学文综试题 题型：044

    已知数列{an}是等差数列，cn＝an2－(n∈N*)

    (1)判断数列{cn}是否是等差数列，并说明理由；

    (2)如果a1＋a3＋…＋a25＝130，a2＋a4＋…＋a26＝143－13k(k为常数)，试写出数列{cn}的通项公式；

    (3)在(2)的条件下，若数列{cn}得前n项和为Sn，问是否存在这样的实数k，使Sn当且仅当n＝12时取得最大值．若存在，求出k的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

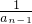    已知数列{an}中a1=数学公式，an=2-数学公式（n≥2，n∈N*），数列 {bn}，满足bn=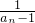数学公式（n∈N*），
    （1）求证数列 {bn}是等差数列；
    （2）若sn=（a1-1）•（a2-1）+（a2-1）•（a3-1）+…+（an-1）•（an+1-1）是否存在a与b∈Z，使得：a≤sn≤b恒成立．若有，求出a的最大值与b的最小值，如果没有，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：辽宁省月考题 题型：解答题

    已知数列{an}中a1=，an=2﹣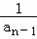（n≥2，n∈N+），数列{bn}，满足bn=（n∈N+），
    （1）求证数列 {bn}是等差数列；
    （2）若sn=（a1﹣1）（a2﹣1）+（a2﹣1）（a3﹣1）+…+（an﹣1）（a n+1﹣1）是否存在a与b∈Z，使得：a≤sn≤b恒成立．若有，求出a的最大值与b的最小值，如果没有，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年辽宁省沈阳二中高三（上）11月月考数学试卷（理科）（解析版） 题型：解答题

    已知数列{an}中a1=，an=2-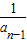（n≥2，n∈N*），数列 {bn}，满足bn=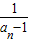（n∈N*），
    （1）求证数列 {bn}是等差数列；
    （2）若sn=（a1-1）•（a2-1）+（a2-1）•（a3-1）+…+（an-1）•（an+1-1）是否存在a与b∈Z，使得：a≤sn≤b恒成立．若有，求出a的最大值与b的最小值，如果没有，请说明理由．

    查看答案和解析>>


    同步练习册答案