若向量 =( =( ,sinα), ,sinα), =(cosα, =(cosα, ),且 ),且 ,则锐角α为 ,则锐角α为 |
A.30°
B.45°
C.60°
D.75° |
相关习题
科目:高中数学
来源:0124 模拟题
题型:单选题
若向量

=(
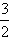
,sinα),

=(cosα,

),且
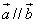
,则锐角α为
A.30°
B.45°
C.60°
D.75°
查看答案和解析>>
科目:高中数学
来源:
题型:
若向量
=(cosα,sinα),
=(cosβ,sinβ),且α-β=kπ(k∈Z),则
与
一定满足:①
与
夹角等于α-β;②|
|=|
|;③
∥;④
⊥.其中正确结论的序号为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
若向量
=(,sinθ),=(cosθ,),且
∥
,则锐角θ等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若向量
=(,sinθ),=(cosθ,),且
∥,则锐角θ等于( )
查看答案和解析>>
科目:高中数学
来源:2008-2009学年广东省深圳市翠园中学、宝安中学联考高三(上)期中数学试卷(理科)(解析版)
题型:解答题
设

=(cosα,(λ-1)sinα),

=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且

与

互相垂直.
(1)求λ的值;
(2)若

=

,tanβ=

,求tanα的值.
查看答案和解析>>
科目:高中数学
来源:2013年高考数学复习卷B(三)(解析版)
题型:解答题
设
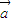
=(cosα,(λ-1)sinα),

=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
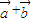
与
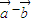
互相垂直.
(1)求λ的值;
(2)若

=
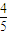
,tanβ=

,求tanα的值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知α∈(
,π),向量
=(sin,1),
=(1,cos),且
•=(1)求cosα的值;
(2)若sin(α+β)=-
,β∈(0,
),求sinβ的值.
查看答案和解析>>
科目:高中数学
来源:
题型:
设
=(cosα,(λ-1)sinα),
=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
+与
-互相垂直.
(1)求λ的值;
(2)若
• =
,tanβ=
,求tanα的值.
查看答案和解析>>
科目:高中数学
来源:湖南省长沙市一中2010届高三第三次月考(理)
题型:解答题
已知向量
(1)求cos (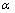 –
–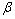 )的值;
)的值;
(2)若0<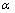 <
< ,–
,– <
<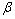 <0,且sin
<0,且sin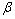 =
= ,求sin
,求sin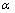 .
.
查看答案和解析>>

 =(cosα,(λ-1)sinα),
=(cosα,(λ-1)sinα), =(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且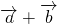 与
与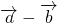 互相垂直.
互相垂直.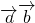 =
= ,tanβ=
,tanβ= ,求tanα的值.
,求tanα的值. =(cosα,(λ-1)sinα),
=(cosα,(λ-1)sinα), =(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且 与
与 互相垂直.
互相垂直. =
= ,tanβ=
,tanβ= ,求tanα的值.
,求tanα的值.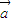 =(cosα,(λ-1)sinα),
=(cosα,(λ-1)sinα), =(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且
=(cosβ,sinβ)(λ>0,0<α<β<π)是平面上的两个向量,且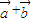 与
与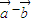 互相垂直.
互相垂直. =
=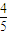 ,tanβ=
,tanβ= ,求tanα的值.
,求tanα的值.