
已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足a1=f(0),且f(an+1)= (n∈N*),则a2011的值为 (n∈N*),则a2011的值为 |
A.4017 B.4018 C.4019 D.4021 |
科目:高中数学 来源:不详 题型:单选题
 ,则a2011的值为
,则a2011的值为| A.4017 | B.4018 | C.4019 | D.4021 |
科目:高中数学 来源:0127 模拟题 题型:单选题
 (n∈N*),则a2011的值为
(n∈N*),则a2011的值为科目:高中数学 来源: 题型:
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立,f(3)=-3.
(1)证明:函数y=f(x)是R上的减函数;
(2)证明:函数y=f(x)是奇函数;
(3)试求函数y=f(x)在[m,n](m,n∈Z)上的值域.
科目:高中数学 来源: 题型:
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立,f(3)=-3.
(1)证明:函数y=f(x)是R上的减函数;
(2)证明:函数y=f(x)是奇函数;
(3)试求函数y=f(x)在[m,n](m,n∈Z)上的值域.
科目:高中数学 来源:0113 期末题 题型:证明题
科目:高中数学 来源:不详 题型:解答题
科目:高中数学 来源:高三数学教学与测试 题型:044
(1)已知函数y=f(x)的定义域为R,且当x∈R时,f(m+x)=f(m-x)恒成立,求证y=f(x)的图象关于直线x=m对称;
(2)若函数y= 的图象的对称轴是x=2,求非零实数a的值.
的图象的对称轴是x=2,求非零实数a的值.
科目:高中数学 来源:最新名师点评测试卷 高一数学 第一册上 题型:013
已知函数y=f(x)是定义域为R的偶函数,当x<0时,函数f(x)单调递增,且有f(x)<0,若f(0)=0,则下列不等式:
①-f(-2)>-f(-1)>f(1)>f(2);
②f(-2)<f(-1)<f![]() ;
;
③f(-4)<f(-2)<-f(3)<-f(5);
④f(-2)<f(-1)<-f(3)<-f(4).
其中正确的个数是
[ ]
科目:高中数学 来源: 题型:013
已知函数
y=f(x)是定义域为R的偶函数,当x<0时,函数f(x)单调递增,且有f(x)<0,若f(0)=0,则下列不等式:①-
f(-2)>-f(-1)>f(1)>f(2);②
f(-2)<f(-1)<f③
f(-4)<f(-2)<-f(3)<-f(5);④
f(-2)<f(-1)<-f(3)<-f(4).其中正确的个数是
[ ]
|
A .1 |
B .2 |
C .3 |
D .4 |
科目:高中数学 来源:2011-2012学年河南省高三第三次大考理科数学 题型:选择题
已知函数y=f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x+x2,若存在正数a,b,使得当x∈[a,b]时,f(x)的值域为[ ],则a+b=
],则a+b=
A.1 B.
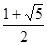 C.
C.
 D.
D.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com