设函数f(x)=sin(2x+ )cos(2x+ )cos(2x+ ) ) |
A.y=f(x)在 单调递增,其图像关于直线 单调递增,其图像关于直线 对称 对称
B.y=f(x)在 单调递增,其图像关于直线 单调递增,其图像关于直线 对称 对称
C.y=f(x)在 单调递减,其图像关于直线 单调递减,其图像关于直线 对称 对称
D.y=f(x)在 单调递减,其图像关于直线 单调递减,其图像关于直线 对称 对称 |
相关习题
科目:高中数学
来源:专项题
题型:单选题
设函数f(x)=sin(2x+

)cos(2x+

)
A.y=f(x)在
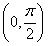
单调递增,其图像关于直线

对称
B.y=f(x)在
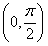
单调递增,其图像关于直线
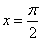
对称
C.y=f(x)在
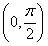
单调递减,其图像关于直线

对称
D.y=f(x)在
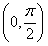
单调递减,其图像关于直线

对称
查看答案和解析>>
科目:高中数学
来源:河北省模拟题
题型:单选题
设函数f(x)=

cos(2x+φ)+sin(2x+φ)

,且其图象关于直线x=0对称,则
A、y=f(x)的最小正周期为π,且在

上为增函数
B、y=f(x)的最小正周期为π,且在

上为减函数
C、y=f(x)的最小正周期为

,且在

上为增函数
D、y=f(x)的最小正周期为
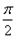
,且在
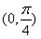
上为减函数
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求
g(α+)的值.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x1是f(x)的一个极大值点,x2上g(x)的一个极小值点,求|x1-x2|的最小值;
(2)若f′(α)=g′(α),求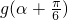 的值.
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求
g(α+)的值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年江西省南昌三中高三(上)第二次月考数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求

的值.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省金华市兰溪一中高二(下)期中数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求
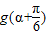
的值.
查看答案和解析>>
科目:高中数学
来源:2011年江西省高考数学仿真押题卷05(理科)(解析版)
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求

的值.
查看答案和解析>>
科目:高中数学
来源:2011年江苏省连云港市东海高级中学高考数学三模试卷(解析版)
题型:解答题
已知函数f(x)=sin(2x+φ)+1和g(x)=cos(2x+φ).
(1)设x
1是f(x)的一个极大值点,x
2上g(x)的一个极小值点,求|x
1-x
2|的最小值;
(2)若f′(α)=g′(α),求

的值.
查看答案和解析>>
科目:高中数学
来源:金山区一模
题型:解答题
设函数f(x)=
.
(1)化简f(x)的表达式,求f(x)的定义域,并求出f(x)的最大值和最小值;
(2)若锐角α满足cosα=
,求f(α)的值.
查看答案和解析>>

 )cos(2x+
)cos(2x+ )
) 单调递增,其图像关于直线
单调递增,其图像关于直线 对称
对称 单调递增,其图像关于直线
单调递增,其图像关于直线 对称
对称 单调递减,其图像关于直线
单调递减,其图像关于直线 对称
对称 单调递减,其图像关于直线
单调递减,其图像关于直线 对称
对称 )cos(2x+
)cos(2x+ )
)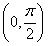 单调递增,其图像关于直线
单调递增,其图像关于直线 对称
对称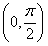 单调递增,其图像关于直线
单调递增,其图像关于直线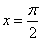 对称
对称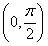 单调递减,其图像关于直线
单调递减,其图像关于直线 对称
对称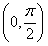 单调递减,其图像关于直线
单调递减,其图像关于直线 对称
对称 cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ) ,且其图象关于直线x=0对称,则
,且其图象关于直线x=0对称,则 上为增函数
上为增函数 上为减函数
上为减函数 ,且在
,且在 上为增函数
上为增函数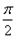 ,且在
,且在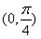 上为减函数
上为减函数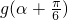 的值.
的值. 的值.
的值.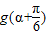 的值.
的值. 的值.
的值. 的值.
的值.