
| 如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有 |
|
A.24种 B.18种 C.16种 D.12种 |
科目:高中数学 来源: 题型:
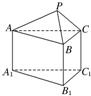 5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
5、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )科目:高中数学 来源: 题型:
 8、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有
8、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有
科目:高中数学 来源:2011年高考数学复习:11.1 分类加法计数原理与分步乘法计数原理1(理科)(解析版) 题型:解答题

科目:高中数学 来源:2011年高考数学复习:11.1 分类加法计数原理与分步乘法计数原理2(理科)(解析版) 题型:选择题

科目:高中数学 来源: 题型:填空题
 如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有 ________种.
如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有 ________种.科目:高中数学 来源:同步题 题型:单选题

科目:高中数学 来源: 题型:解答题
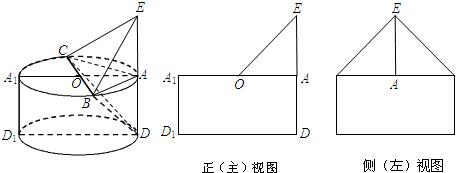
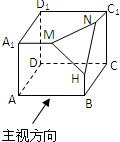 如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.
如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.科目:高中数学 来源:2012年上海市黄浦区、嘉定区高考数学二模试卷(文科)(解析版) 题型:解答题
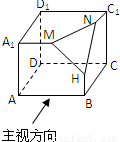
科目:高中数学 来源: 题型:
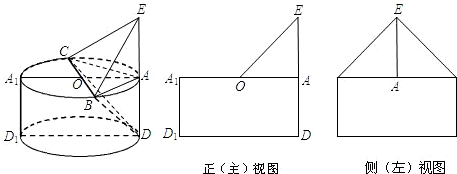
科目:高中数学 来源: 题型:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com