| 已知M为直线l1:y=x+2上任一点,点N(-1,0),则过点M,N且与直线l2:x=1相切的圆的个数可能为 |
A.0或1
B.1或2
C.0,1或2
D.2 |
相关习题
科目:高中数学
来源:专项题
题型:单选题
已知M为直线l1:y=x+2上任一点,点N(-1,0),则过点M,N且与直线l2:x=1相切的圆的个数可能为
A.0或1
B.1或2
C.0,1或2
D.2
查看答案和解析>>
科目:高中数学
来源:
题型:
已知M为直线l1:y=x+2上任意一点,点N(-1,0),则过点M,N且与直线l2:x=1相切的圆的个数可能为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知直线l1:mx-y=0,l2:x+my-m-2=0
(1)求证:直线l2恒过定点,并求定点坐标;
(2)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(3)若l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,求当实数m取值变化时,△MP1P2面积取得最大值时,直线l1的方程.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知:动点P(x,y)到点F(0,1)的距离比它到直线y+2=0的距离小1,
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)在直线y=-1上任取一点M作曲线C的两条切线l1,l2,切点分别为A,B,在y轴上是否存在定点Q,使△ABQ的内切圆圆心在定直线n上?若存在,求出点Q的坐标及定直线n的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知直线l1:mx-y=0,l2:x+my-m-2=0
(1)求证:直线l2恒过定点,并求定点坐标;
(2)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(3)若l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,求当实数m取值变化时,△MP1P2面积取得最大值时,直线l1的方程.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省宁波市金兰合作组织高二(上)期中数学试卷(理科)(解析版)
题型:解答题
已知直线l1:mx-y=0,l2:x+my-m-2=0
(1)求证:直线l2恒过定点,并求定点坐标;
(2)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(3)若l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,求当实数m取值变化时,△MP1P2面积取得最大值时,直线l1的方程.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省宁波市金兰合作组织高二(上)期中数学试卷(理科)(解析版)
题型:解答题
已知直线l1:mx-y=0,l2:x+my-m-2=0
(1)求证:直线l2恒过定点,并求定点坐标;
(2)求证:对m的任意实数值,l1和l2的交点M总在一个定圆上;
(3)若l1与定圆的另一个交点为P1,l2与定圆的另一个交点为P2,求当实数m取值变化时,△MP1P2面积取得最大值时,直线l1的方程.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年山东省济南外国语学校高三(下)3月质量检测数学试卷(文科)(解析版)
题型:解答题
已知
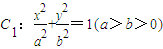
的离心率为
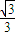
,直线l:x-y=0与以原点为圆心,以椭圆C
1的短半轴长为半径的圆相切,曲线C
2以x轴为对称轴.
(1)求椭圆C
1的方程;
(2)设椭圆C
1的左焦点为F
1,右焦点F
2,直线l
1过点F
1且垂直于椭圆的长轴,曲线C
2上任意一点M到l
1距离与MF
2相等,求曲线C
2的方程.
(3)若A(x
1,2),C(x
,y
),是C
2上不同的点,且AB⊥BC,求y
的取值范围.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年山东省济南外国语学校高三(下)3月质量检测数学试卷(理科)(解析版)
题型:解答题
已知
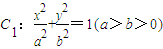
的离心率为

,直线l:x-y=0与以原点为圆心,以椭圆C
1的短半轴长为半径的圆相切,曲线C
2以x轴为对称轴.
(1)求椭圆C
1的方程;
(2)设椭圆C
1的左焦点为F
1,右焦点F
2,直线l
1过点F
1且垂直于椭圆的长轴,曲线C
2上任意一点M到l
1距离与MF
2相等,求曲线C
2的方程.
(3)若A(x
1,2),C(x
,y
),是C
2上不同的点,且AB⊥BC,求y
的取值范围.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年浙江省舟山市七校高三(下)3月联考数学试卷(理科)(解析版)
题型:解答题
已知

的离心率为

,直线l:x-y=0与以原点为圆心,以椭圆C
1的短半轴长为半径的圆相切,曲线C
2以x轴为对称轴.
(1)求椭圆C
1的方程;
(2)设椭圆C
1的左焦点为F
1,右焦点F
2,直线l
1过点F
1且垂直于椭圆的长轴,曲线C
2上任意一点M到l
1距离与MF
2相等,求曲线C
2的方程.
(3)若A(x
1,2),C(x
,y
),是C
2上不同的点,且AB⊥BC,求y
的取值范围.
查看答案和解析>>

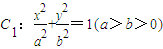 的离心率为
的离心率为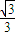 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.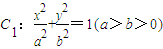 的离心率为
的离心率为 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴. 的离心率为
的离心率为 ,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.
,直线l:x-y=0与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切,曲线C2以x轴为对称轴.