
科目:初中数学 来源: 题型:
 25、七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形.
25、七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形.
科目:初中数学 来源: 题型:解答题
 七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形
七巧板是我们祖先创造的一种智力玩具,如图,整副七巧板是由一个正方形分割成七小块而成(其中:五块等腰直角三角形、一块正方形和一块平行四边形),用这七小块可以拼出各种各样的漂亮图案.请用这七小块拼出一个等腰梯形,并在网格中画出图形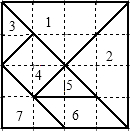
科目:初中数学 来源:不详 题型:解答题
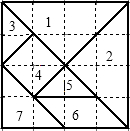

科目:初中数学 来源: 题型:
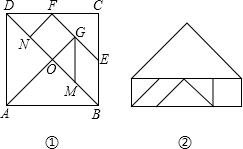 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:解答题
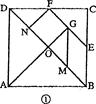
 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
科目:初中数学 来源:浙江省中考真题 题型:解答题


科目:初中数学 来源:浙江省宁波市2006年初中毕业生学业考试数学试题 题型:044
对正方形ABCD分划如图,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.

(1)如果设正方形OGFN的边长为1,这七块部件的各边长中,从小到大的四个不同值分别为1、x1、x2、x3,那么x1=________;各内角中最小内角是________度,最大内角是________度;用它们拼成的一个五边形如图,其面积是________,
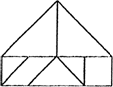
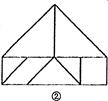
(2)请用这副七巧板,既不留下一丝空自,又不相互重叠,拼出2种边数不同的凸多边形,画在下面格点图中,并使凸多边形的顶点落在格点图的小黑点上(格点图中,上下、左右相邻两点距离都为1).

(3)某合作学习小组在玩七巧板时发现:“七巧板拼成的凸多边形,其边数不能超过8”.你认为这个结论正确吗?请说明理由.
注:不能拼成与图①或②全等的多边形!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com