练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=x2在点x=1处的导数是（　　）
    A．0B．1C．2D．3
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    函数y=x2在点x=1处的导数是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数y=x2在点x=1处的导数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    lnx+kex
    （k为常数，e=2.71828…是自然对数的底数），曲线y=f（x） 在点（1，f（1））处的切线与x轴平行．
    （Ⅰ）求k的值；
    （Ⅱ）求f（x）的单调区间；
    （Ⅲ）设g（x）=（x2+x）f′（x），其中f′（x）是f（x）的导函数．证明：对任意x＞0，g（x）＜1+e-2．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数f（x）=
    lnx+k
    ex
    （k为常数，e=2.71828…是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与x轴平行．
    （Ⅰ）求k的值；
    （Ⅱ）求f（x）的单调区间；
    （Ⅲ）设g（x）=（x2+x）f′（x），其中f′（x）是f（x）的导函数．证明：对任意x＞0，g（x）＜1+e-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网函数y=f（x），x∈[-5，5]的图象如图所示，该曲线在原点处的切线的方程为y=x，且导函数f′（x）是减函数．给出下列四个命题：
    ①A，B是该图象上的任意两点，那么直线AB的斜率kAB∈（0，1）；
    ②点P是该图象在第一象限内的部分上的点，那么直线OP的斜率kOP∈（0，1）；
    ③对于?x1，x2∈[-5，5]，f（x1）+f（x2）≤2f（
    x1+x2
    2
    ）恒成立；
    ④对于?x∈[-5，5]，f（x）≤x．
    其中所有真命题的序号是（　　）
    A、①②③B、②③④
    C、②④D、①③

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年北京市海淀区高二（下）期中数学试卷（理科）（解析版） 题型：选择题

    函数y=f（x），x∈[-5，5]的图象如图所示，该曲线在原点处的切线的方程为y=x，且导函数f′（x）是减函数．给出下列四个命题：
    ①A，B是该图象上的任意两点，那么直线AB的斜率kAB∈（0，1）；
    ②点P是该图象在第一象限内的部分上的点，那么直线OP的斜率kOP∈（0，1）；
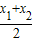    ③对于?x1，x2∈[-5，5]，f（x1）+f（x2）≤2f（）恒成立；
    ④对于?x∈[-5，5]，f（x）≤x．
    其中所有真命题的序号是（ ）

    A．①②③
    B．②③④
    C．②④
    D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

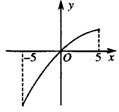    函数y=f（x），x∈[-5，5]的图象如图所示，该曲线在原点处的切线的方程为y=x，且导函数f′（x）是减函数．给出下列四个命题：
    ①A，B是该图象上的任意两点，那么直线AB的斜率kAB∈（0，1）；
    ②点P是该图象在第一象限内的部分上的点，那么直线OP的斜率kOP∈（0，1）；
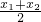    ③对于?x1，x2∈[-5，5]，f（x1）+f（x2）≤2f（数学公式）恒成立；
    ④对于?x∈[-5，5]，f（x）≤x．
    其中所有真命题的序号是


    1. A.
      ①②③
    2. B.
      ②③④
    3. C.
      ②④
    4. D.
      ①③

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖南省、岳阳县一中高三11月联考理科数学 题型：解答题

    （本小题满分13分）(第一问8分，第二问5分)

    已知函数f(x)＝2lnx，g(x)＝ax2＋3x.

    （1）设直线x＝1与曲线y＝f(x)和y＝g(x)分别相交于点P、Q，且曲线y＝f(x)和y＝g(x)在点P、Q处的切线平行，若方程f(x2＋1)＋g(x)＝3x＋k有四个不同的实根，求实数k的取值范围；

    （2）设函数F(x)满足F(x)＋x［f′(x)－g′(x)］＝－3x2－(a＋6)x＋1.其中f′(x)，g′(x)分别是函数f(x)与g(x)的导函数；试问是否存在实数a，使得当x∈(0,1］时，F(x)取得最大值，若存在，求出a的取值范围；若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2012届湖南省澧县一中、岳阳县一中高三11月联考理科数学 题型：解答题

    （本小题满分13分）(第一问8分，第二问5分)
    已知函数f(x)＝2lnx，g(x)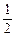＝ax2＋3x.
    （1）设直线x＝1与曲线y＝f(x)和y＝g(x)分别相交于点P、Q，且曲线y＝f(x)和y＝g(x)在点P、Q处的切线平行，若方程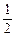f(x2＋1)＋g(x)＝3x＋k有四个不同的实根，求实数k的取值范围；
    （2）设函数F(x)满足F(x)＋x［f′(x)－g′(x)］＝－3x2－(a＋6)x＋1.其中f′(x)，g′(x)分别是函数f(x)与g(x)的导函数；试问是否存在实数a，使得当x∈(0,1］时，F(x)取得最大值，若存在，求出a的取值范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分13分）(第一问8分，第二问5分)
    已知函数f(x)＝2lnx，g(x)＝ax2＋3x.
    （1）设直线x＝1与曲线y＝f(x)和y＝g(x)分别相交于点P、Q，且曲线y＝f(x)和y＝g(x)在点P、Q处的切线平行，若方程f(x2＋1)＋g(x)＝3x＋k有四个不同的实根，求实数k的取值范围；
    （2）设函数F(x)满足F(x)＋x［f′(x)－g′(x)］＝－3x2－(a＋6)x＋1.其中f′(x)，g′(x)分别是函数f(x)与g(x)的导函数；试问是否存在实数a，使得当x∈(0,1］时，F(x)取得最大值，若存在，求出a的取值范围；若不存在，说明理由.

    查看答案和解析>>


    同步练习册答案